Getting Physics-Relevant Information
Overview
Teaching: 20 min
Exercises: 10 minQuestions
How can I use columnar analysis to do something useful for physics?
Objectives
Find dimuon invariant mass resonances.
Okay, we’re finally ready to look for resonances in dimuon events.
We need a mask that selects events with exactly two muons:
two_muons_mask = branches['nMuon'] == 2
Now we need to construct the four-momenta of each muon.
Vector is a package that provides an interface to operate on 2D, 3D, and 4D vectors.
We can get the four-momenta of all muons in the tree by using vector.zip and passing it the pT, eta, phi, and mass arrays:
import vector
muon_p4 = vector.zip({'pt': branches['Muon_pt'], 'eta': branches['Muon_eta'], 'phi': branches['Muon_phi'], 'mass': branches['Muon_mass']})
We’ll go ahead and filter out events that don’t contain exactly two muons:
two_muons_p4 = muon_p4[two_muons_mask]
Then let’s take a look at it:
two_muons_p4
<MomentumArray4D [[{rho: 10.8, ... tau: 0.106}]] type='48976 * var * Momentum4D[...'>
This is an array of 4D momenta. We can get the components back out with these properties:
two_muons_p4.pt
two_muons_p4.eta
two_muons_p4.phi
two_muons_p4.E
two_muons_p4.mass
What we want is the invariant mass of the two muons in each of these events. To do that, we need the sum of their four-vectors. First, we pick out the first muon in each event with 2D slice:
first_muon_p4 = two_muons_p4[:, 0]
In the notation [:, 0], : means “include every row in the first dimension” (i.e., all events in the array).
The comma separates the selection along the first dimension from the selection along the second dimension.
The second dimension is the muons in each event, so we want the first, or the one at the 0 index.
Then we do the same to get the second muon in each event, just changing the 0 index to 1:
second_muon_p4 = two_muons_p4[:, 1]
DeltaR
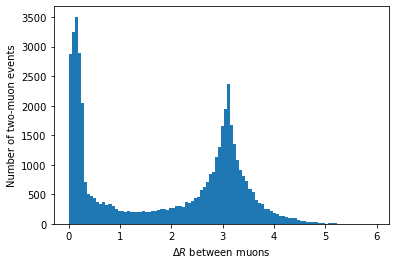
Another useful feature of these four-vector arrays is being able to compute deltaR (= sqrt(deltaEta^2 + deltaPhi^2)):
first_muon_p4.deltaR(second_muon_p4)plt.hist(first_muon_p4.deltaR(second_muon_p4), bins=100) plt.xlabel('$\Delta R$ between muons') plt.ylabel('Number of two-muon events') plt.show()
In principle, we could use this to clean up our invariant mass distribution, but we’ll skip that for simplicity.
Adding the four-vectors of the first muon and the second muon for all events is really as easy as:
sum_p4 = first_muon_p4 + second_muon_p4
sum_p4
<MomentumArray4D [{rho: 8.79, phi: 1.83, ... tau: 16.5}] type='48976 * Momentum4...'>
This is a 1D array of the four-vector sum for each event.
The last thing we need to do before we’re ready to plot the spectrum is to select only pairs with opposite charges:
two_muons_charges = branches['Muon_charge'][two_muons_mask]
opposite_sign_muons_mask = two_muons_charges[:, 0] != two_muons_charges[:, 1]
We apply this selection to the four-vector sums to get the dimuon four-vectors:
dimuon_p4 = sum_p4[opposite_sign_muons_mask]
Exercise
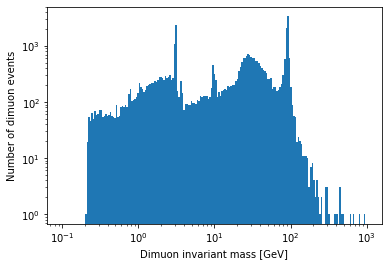
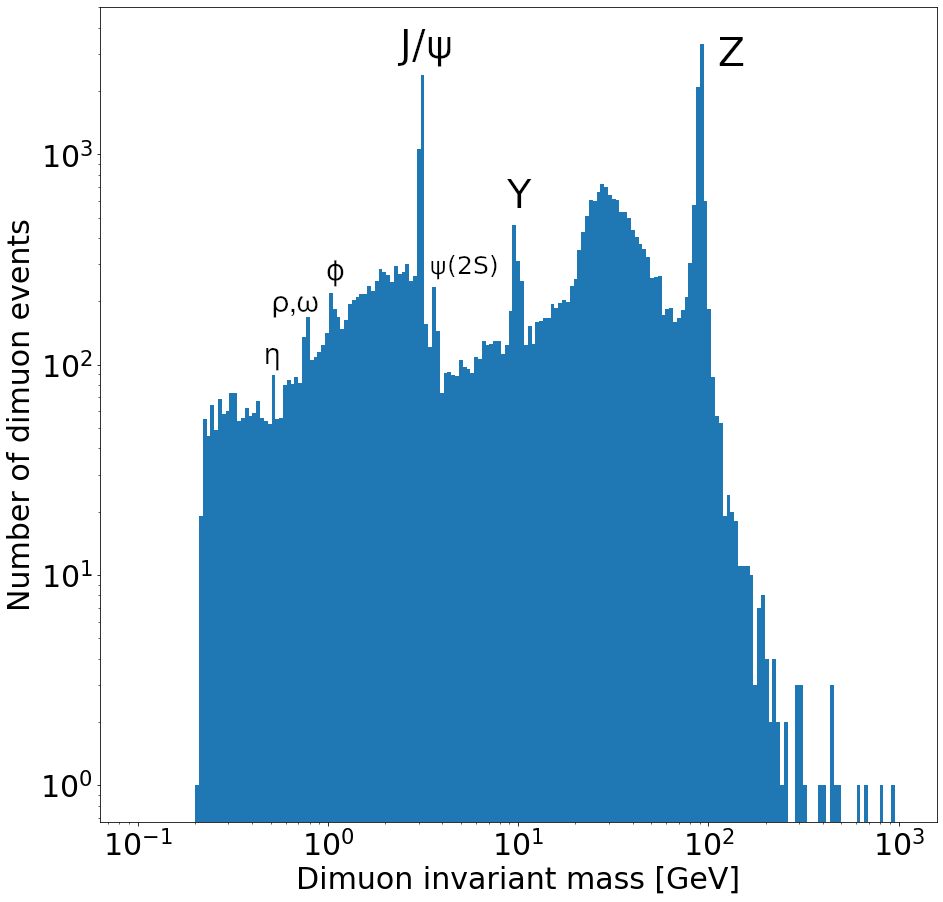
Plot a histogram of the dimuon invariant mass on a log-log plot. Try to find all resonances (there are at least 7 visible). How many dimuon events are there?
Solution
plt.hist(dimuon_p4.mass, bins=np.logspace(np.log10(0.1), np.log10(1000), 200)) plt.xlabel('Dimuon invariant mass [GeV]') plt.ylabel('Number of dimuon events') plt.xscale('log') plt.yscale('log') plt.show()
Labeled resonances:
len(dimuon_p4)37183
Key Points
Vector has allows you to manipulate arrays of four-vectors.
Uproot can be used to do real physics analyses.