Solutions (NO PEEKING!)#
Do not look at this section until you have attempted to solve the problem yourself.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torch
from torch import nn, optim
from torch.utils.data import TensorDataset, DataLoader, random_split
expected_ROC = np.array([
[0, 0.01886829927], [0.0001020304051, 0.1289489538],
[0.0004081216202, 0.209922966 ], [0.0009182736455, 0.3068408332],
[0.001632486481, 0.376408661 ], [0.002550760127, 0.4303733732],
[0.003673094582, 0.4678969334 ], [0.004999489848, 0.5027722976],
[0.006529945924, 0.526339701 ], [0.00826446281, 0.5538282184],
[0.01020304051, 0.5764214002 ], [0.01234567901, 0.6020473392],
[0.01469237833, 0.6217746216 ], [0.01724313846, 0.6441249222],
[0.01999795939, 0.6616243646 ], [0.02295684114, 0.6776505449],
[0.0261197837, 0.6922878624 ], [0.02948678706, 0.7049561472],
[0.03305785124, 0.7174712901 ], [0.03683297623, 0.7281837347],
[0.04081216202, 0.7378146857 ], [0.04499540863, 0.7487390868],
[0.04938271605, 0.7581570351 ], [0.05397408428, 0.7678773984],
[0.05876951331, 0.7770101384 ], [0.06376900316, 0.7856509131],
[0.06897255382, 0.7942924103 ], [0.07438016529, 0.8015956393],
[0.07999183757, 0.8080126115 ], [0.08580757066, 0.8131647638],
[0.09182736455, 0.8193828345 ], [0.09805121926, 0.8250768418],
[0.1044791348, 0.8305736234 ], [0.1111111111, 0.8350616401],
[0.1179471483, 0.8392843805 ], [0.1249872462, 0.843458635 ],
[0.132231405, 0.8485805236 ], [0.1396796245, 0.8527170936],
[0.1473319049, 0.8568358996 ], [0.1551882461, 0.8609808587],
[0.1632486481, 0.8650308152 ], [0.1715131109, 0.8690270267],
[0.1799816345, 0.8728376092 ], [0.188654219, 0.8768071621],
[0.1975308642, 0.8809618493 ], [0.2066115702, 0.8844406165],
[0.2158963371, 0.8878818684 ], [0.2253851648, 0.8913015608],
[0.2350780533, 0.895321326 ], [0.2449750026, 0.8988141059],
[0.2550760127, 0.9023606647 ], [0.2653810836, 0.9060166576],
[0.2758902153, 0.9095274507 ], [0.2866034078, 0.9131203545],
[0.2975206612, 0.9160367475 ], [0.3086419753, 0.9194866744],
[0.3199673503, 0.9227445269 ], [0.331496786, 0.9258525464],
[0.3432302826, 0.9288425431 ], [0.35516784, 0.9320369642],
[0.3673094582, 0.934770168 ], [0.3796551372, 0.937793916 ],
[0.3922048771, 0.9407399938 ], [0.4049586777, 0.9435231388],
[0.4179165391, 0.946281785 ], [0.4310784614, 0.9488092479],
[0.4444444444, 0.9518475898 ], [0.4580144883, 0.9547152601],
[0.471788593, 0.9572437037 ], [0.4857667585, 0.959630249 ],
[0.4999489848, 0.9625112252 ], [0.5143352719, 0.9647093883],
[0.5289256198, 0.9668044304 ], [0.5437200286, 0.9689679766],
[0.5587184981, 0.9712781888 ], [0.5739210285, 0.9728035781],
[0.5893276196, 0.9748502201 ], [0.6049382716, 0.9769168758],
[0.6207529844, 0.9783125007 ], [0.636771758, 0.9804721129],
[0.6529945924, 0.982129956 ], [0.6694214876, 0.9841034064],
[0.6860524436, 0.9858651034 ], [0.7028874605, 0.9875667363],
[0.7199265381, 0.9892142364 ], [0.7371696766, 0.9907125562],
[0.7546168758, 0.9919437219 ], [0.7722681359, 0.9932740291],
[0.7901234568, 0.9942632436 ], [0.8081828385, 0.9954980595],
[0.826446281, 0.9962563498 ], [0.8449137843, 0.9970929737],
[0.8635853484, 0.9977009724 ], [0.8824609734, 0.9984200208],
[0.9015406591, 0.9988781108 ], [0.9208244057, 0.9991514607],
[0.940312213, 0.9994587815 ], [0.9600040812, 0.999709012 ],
[0.9799000102, 0.9998581822 ], [1, 1 ],
])
Step 1: download and understand the data#
hls4ml_lhc_jets_hlf = pd.read_parquet("data/hls4ml_lhc_jets_hlf.parquet")
features = hls4ml_lhc_jets_hlf.drop("jet_type", axis=1)
targets = hls4ml_lhc_jets_hlf["jet_type"]
Step 2: split the data into training, validation, and test samples#
dataset = torch.utils.data.TensorDataset(
torch.tensor(features.values, dtype=torch.float32),
torch.tensor(targets.cat.codes.values, dtype=torch.int64),
)
subset_train, subset_valid, subset_test = torch.utils.data.random_split(dataset, [0.8, 0.1, 0.1])
Step 3: build a classifier neural network#
Not all of the features are close to the interval \((-1, 1)\), so you needed to scale each column to have zero mean and unit standard deviation.
Since this is a machine-optimized part of the fit, let’s use only the training sample to determine the mean and standard deviation of each feature.
class ScaleInputs(nn.Module):
def __init__(self, subset_train):
super().__init__()
# get a single features tensor for the whole training subset
((features_tensor, targets_tensor),) = DataLoader(subset_train, batch_size=len(targets))
# get 16 means and 16 standard deviations from the training dataset
self.register_buffer("means", features_tensor.mean(axis=0))
self.register_buffer("stds", features_tensor.std(axis=0))
def forward(self, x):
return (x - self.means) / self.stds
scale_inputs = ScaleInputs(subset_train)
model_without_softmax = nn.Sequential(
scale_inputs,
nn.Linear(16, 32), # 16 input features → a hidden layer with 32 neurons
nn.ReLU(), # ReLU avoids the vanishing gradients problem
nn.Linear(32, 32), # first hidden layer → second hidden layer
nn.ReLU(),
nn.Linear(32, 32), # second hidden layer → third hidden layer
nn.ReLU(),
nn.Linear(32, 5), # third hidden layer → 5 output category probabilities
# no softmax because CrossEntropyLoss automatically applies it
)
Step 4: monitor the loss function#
The following fits the model with loss function monitoring integrated into the loop.
NUM_EPOCHS = 10
BATCH_SIZE = 20000
# DataLoader lets us iterate over mini-batches, given a Subset
train_loader = DataLoader(subset_train, batch_size=BATCH_SIZE)
# the validation sample doesn't need to be batched, so we make it one big batch
valid_loader = DataLoader(subset_valid, batch_size=len(subset_valid))
loss_function = nn.CrossEntropyLoss()
optimizer = optim.Adam(model_without_softmax.parameters(), lr=0.03)
# collect loss data versus epoch
valid_loss_vs_epoch = []
train_loss_vs_epoch = []
for epoch in range(NUM_EPOCHS):
# this asserts that the validation_loader iterates over exactly one batch
((features_tensor, targets_tensor),) = valid_loader
predictions_tensor = model_without_softmax(features_tensor)
loss = loss_function(predictions_tensor, targets_tensor)
valid_loss = loss.item() * len(targets_tensor) * (0.8 / 0.1) # normalize!
valid_loss_vs_epoch.append(valid_loss)
# the training sample needs a mini-batch loop
train_loss = 0
for features_tensor, targets_tensor in train_loader:
optimizer.zero_grad()
predictions_tensor = model_without_softmax(features_tensor)
loss = loss_function(predictions_tensor, targets_tensor)
train_loss += loss.item() * len(targets_tensor) # normalize!
loss.backward()
optimizer.step()
train_loss_vs_epoch.append(train_loss)
# print out partial quantities so we can discover mistakes early
print(f"{epoch = } {train_loss = } {valid_loss = }")
epoch = 0 train_loss = 669897.2902297974 valid_loss = 1067996.2720870972
epoch = 1 train_loss = 519501.20520591736 valid_loss = 544417.8190231323
epoch = 2 train_loss = 493439.3084049225 valid_loss = 500548.1963157654
epoch = 3 train_loss = 474700.7346153259 valid_loss = 486229.93326187134
epoch = 4 train_loss = 465447.77369499207 valid_loss = 471370.6855773926
epoch = 5 train_loss = 454168.0657863617 valid_loss = 461227.92625427246
epoch = 6 train_loss = 453111.8142604828 valid_loss = 452004.5123100281
epoch = 7 train_loss = 444692.2745704651 valid_loss = 446853.581905365
epoch = 8 train_loss = 442660.94279289246 valid_loss = 450847.02920913696
epoch = 9 train_loss = 445633.9588165283 valid_loss = 446701.6043663025
fig, ax = plt.subplots()
ax.plot(range(len(train_loss_vs_epoch)), train_loss_vs_epoch, marker=".")
ax.plot(range(len(valid_loss_vs_epoch)), valid_loss_vs_epoch, marker=".")
ax.grid(True, "both", "y", linestyle=":")
ax.set_xticks(range(NUM_EPOCHS))
ax.set_ylim(0, 1.2*max(max(train_loss_vs_epoch), max(valid_loss_vs_epoch)))
ax.set_xlabel("epoch number")
ax.set_ylabel("loss")
ax.legend(["training sample", "validation sample"])
plt.show()
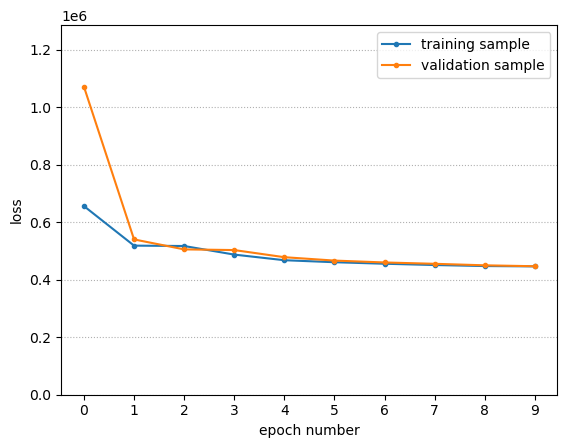
With smaller BATCH_SIZE, it converges to the same final loss in a smaller number of epochs (less total time).
To make the above plot interesting, BATCH_SIZE was chosen larger than it needed to be!
I see no sign of overfitting. This dataset has a lot of data points and they are not degenerate (all laying in a line/plane/hyperplane) and the neural network is not too large for it. There’s no need to add any regularization.
Step 5: compute a 5×5 confusion matrix#
To compute predictions as probabilities, we’ll need to apply the softmax function, so make a new model that has this included.
model_with_softmax = nn.Sequential(
model_without_softmax,
nn.Softmax(dim=1),
)
The first time you make this plot, it should use the validation sample (valid_loader).
Below, I’m using the test sample (test_loader) because I’ve already checked the validation sample and I won’t be making any more changes to my model or fitting procedure.
test_loader = DataLoader(subset_test, batch_size=len(subset_test))
((features_tensor, targets_tensor),) = test_loader
predictions_tensor = model_with_softmax(features_tensor)
confusion_matrix = np.array(
[
[
(predictions_tensor[targets_tensor == true_class].argmax(axis=1) == prediction_class).sum().item()
for prediction_class in range(5)
]
for true_class in range(5)
]
)
confusion_matrix
array([[12886, 2092, 1224, 269, 228],
[ 2597, 11654, 1041, 561, 342],
[ 1267, 538, 13845, 697, 364],
[ 753, 2643, 252, 12589, 400],
[ 840, 2373, 297, 902, 12346]])
A colorbar plot demonstrates the quality of this model: the diagonal (correct predictions) is much more populated than the off-diagonals.
fig, ax = plt.subplots(figsize=(7, 7))
image = ax.imshow(confusion_matrix, vmin=0)
fig.colorbar(image, ax=ax, label="number of test samples", shrink=0.8)
ax.set_xticks(range(5), targets.cat.categories)
ax.set_yticks(range(5), targets.cat.categories)
ax.set_xlabel("predicted jet category")
ax.set_ylabel("true jet category")
None
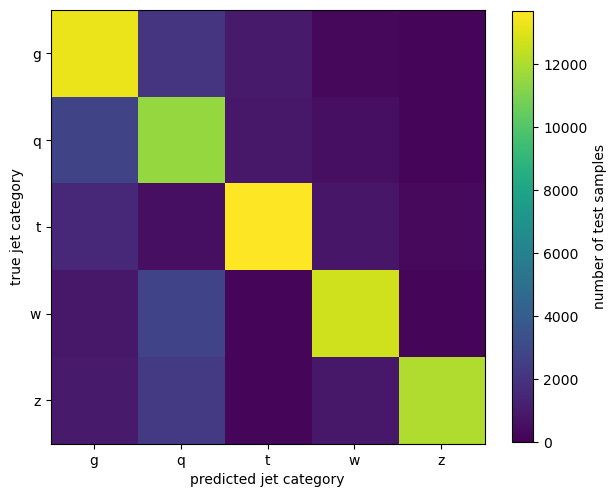
Step 6: project it down to a 2×2 confusion matrix#
The following selects true heavy/electroweak events using is_heavy and determines if the model predicts heavy/electroweak if the sum of the 't', 'w', 'z' probabilities is greater than the threshold.
It would have been entirely equivalent to define a true light/QCD selection as
is_light = (targets_tensor < 2)
and a light/QCD prediction as
selected_predictions[:, 0:2].sum(axis=1) <= threshold
Each (length-5) row vector in the predictions consists of non-overlapping probabilities that add up to 1 (by construction, because of the softmax). So the sum of slice 0:2 is equal to 1 minus the sum of slice 2:5.
def matrix_for_cutoff_decision_at(threshold):
is_heavy = (targets_tensor >= 2)
true_positive = (predictions_tensor[is_heavy][:, 2:5].sum(axis=1) > threshold).sum().item()
false_positive = (predictions_tensor[~is_heavy][:, 2:5].sum(axis=1) > threshold).sum().item()
false_negative = (predictions_tensor[is_heavy][:, 2:5].sum(axis=1) <= threshold).sum().item()
true_negative = (predictions_tensor[~is_heavy][:, 2:5].sum(axis=1) <= threshold).sum().item()
return np.array([
[true_positive, false_positive],
[false_negative, true_negative],
])
matrix_for_cutoff_decision_at(0.5)
array([[42162, 4048],
[ 7944, 28846]])
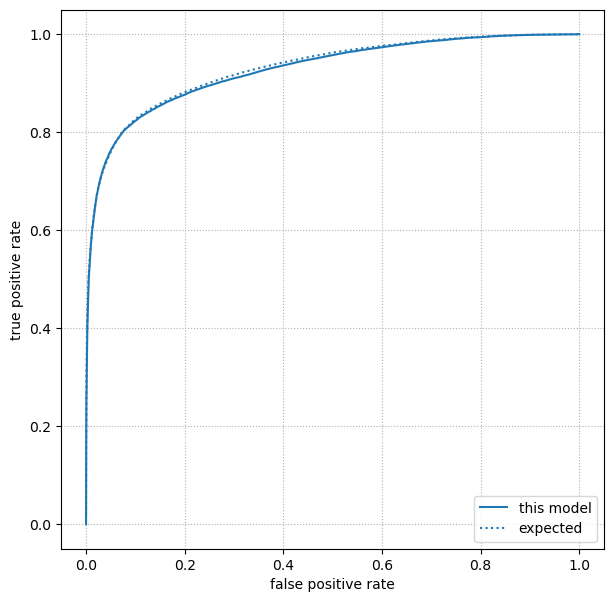
Step 7: plot a ROC curve#
Once we have 2×2 confusion matrices as a function of threshold, we can plot the ROC curve as in the section on Goodness of fit metrics.
true_positive_rates = []
false_positive_rates = []
for threshold in np.linspace(0, 1, 1000):
((true_positive, false_positive),
(false_negative, true_negative)) = matrix_for_cutoff_decision_at(threshold)
true_positive_rates.append(true_positive / (true_positive + false_negative))
false_positive_rates.append(false_positive / (true_negative + false_positive))
fig, ax = plt.subplots(figsize=(7, 7))
ax.plot(false_positive_rates, true_positive_rates, label="this model")
ax.plot(expected_ROC[:, 0], expected_ROC[:, 1], ls=":", color="tab:blue", label="expected")
ax.grid(True, linestyle=":")
ax.set_xlabel("false positive rate")
ax.set_ylabel("true positive rate")
ax.legend(loc="lower right")
plt.show()
