Introduction

Overview

Teaching: 0 min
Exercises: 0 min

Questions

• What is SSH?

• How does SSH encrypt traffic?

• What’s a private/public key?

Objectives

• Understanding asymmetric cryptography

Secure Shell (SSH) is a protocol to access other computers. It was invented in 1995 to make the old methods more secure but, on first glance, it still behaves similar to remote shell or telnet from the eighties: you can connect to a remote computer to enter commands in a terminal. In the simplest case, you will just type the name of the computer you want to connect to:

ssh username@servername.domain

However, SSH has become much more powerful than this if you know how to use it correctly. In the following, we will try to go through all the helpful features you should know when working remotely.

But first we need to talk a bit about security, especially encryption.

Asymmetric Encryption

One cornerstone technology of the current internet is asymmetric cryptography, or public-key cryptography. We all use it constantly without caring about it when browsing the web, but it’s also important for the efficient usage of SSH, so we need to go through some key features of it.

The idea behind asymmetric encryption is to have two distinct, different keys for encryption. One key can encrypt the message and then only the other key can decrypt the message. In practice, we will keep one of these keys private and publish the other.

As an example, let’s say we have two people, Alice and Bob, where Alice owns the private key and Bob has the public key. Then, with this key pair, they can perform two things:

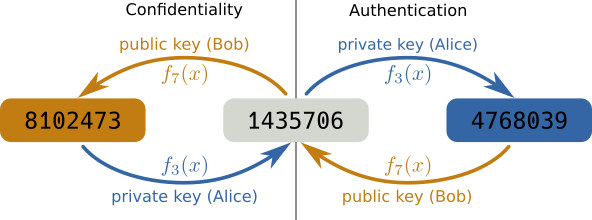
Confidentiality

• Bob can send confidential information only intended for Alice by encrypting it with the public key. Only Alice has the private key to decrypt it and nobody else can see the content of the message (left side of the figure).

Authentication

• To establish the identity of Alice, Bob gives Alice a message to encrypt with her private key. Bob can then decrypt it with his public key to be sure he talks to Alice as only she would have been able to encrypt the message (right side of the figure).
• This is the one you are using almost everywhere in the internet: every https connection on the internet uses this principle to make sure that the server claiming to be “netflix.com” is actually the real Netflix server. And this is also what we use for SSH connections.

Following this example, consider a string of numbers from 1435706. Now for encryption, we could just “add” a value to each of these digits and take the modulus by 10 to get another digit, \(f_{k}(x) = (x + k) \bmod 10\)

Now, if we choose as keys \(A=3\) and \(B=7\), then we can “encrypt” the message by applying \(f_A(x)\) on each digit to get the encrypted message, 4768039. And we can decrypt it again by applying \(f_B(x)\) to get the original message, 1435706. This also works by first applying \(f_B(x)\) and then \(f_A(x)\).

So, if we encrypt a message with one key, we need to use the other key to decrypt the message again and vice versa. Now, this example is obviously way too simple but it is actually rather close to the RSA algorithm still used today.

Warning: Private means private!

While the public key can be shared freely, it is critical that the private key remains private. If someone gains access to your private key they can impersonate you in the digital world and get access to a lot of your resources.

Key Points

• asymmetric cryptography has two keys, a private and a public key.

• it can be used to establish the identity of the owner of the private key.

• the private key should be kept as safe as possible.