Lesson 5: Python on GPUs#
Our introduction to array-oriented programming started by addressing Python’s slowness (or the slowness of interactive environments in general). But GPUs are also best addressed in an array-at-a-time fashion: the memory layout explicitly favors arrays over objects addressed by pointers or references (even in C++). It shouldn’t be a surprise, then, that Python’s GPU libraries are array libraries.
Most users of GPUs in Python are using them for Machine Learning (ML). Since ML libraries are focused on ML, rather than programming in general, they provide an interface that is identical for CPUs and GPUs, usually by a device flag in the array object. (Array objects in ML libraries are called “tensors”… for no good reason.) Switching from device="cpu" to device="cuda" simply speeds up the calculation by an order of magnitude with no other changes.
In this lesson, we’ll focus on GPU programming in which the differences from CPU programming are visible.
The libraries specifically address CUDA, Nvidia’s brand of GPU programming, which reflects the very tight monopoly Nvidia has on GPUs for general-purpose programming. (CuPy has experimental support for AMD but Numba deprecated support for AMD due to lack of community interest. There are Python projects that support OpenCL, Vulkan, Kokkos, and SYCL.) Unfortunately, this excludes many laptops, including all MacOS: CUDA is something you’ll more likely use on a data center than a laptop.
Hints for installing CUDA#
Installing a working version of CUDA can be hard, as it depends strongly on the operating system and GPU hardware. However, here are some hints:
The GPU driver must be installed in the operating system (Windows or Linux) and not with any Python package installers (pip, conda, uv, pixi). You might get it directly from Nvidia or through the operating system’s package installer (such as apt for Ubuntu).
The CUDA compiler and its libraries are distinct from the device driver, and they can be installed with conda. The story is more complicated for CUDA 11, but for CUDA 12, just include
cuda-version=12in the list of packages to install.Nvidia publishes a table of version compatibility between GPU hardware, drivers, and CUDA packages.
Numba comes with a
numba -scommandline tool to print the versions of everything: incompatibilities between driver and CUDA package can be found here.nvidia-smican also be useful.
In this lesson, we’ll be using the cupy and numba packages (same names in pip and conda), which will pull all of the CUDA dependencies they need. So if you have an Nvidia GPU and appropriate drivers installed, this should work:
conda install cuda-version=12 cupy numba
and this acts as a test that it worked (the random numbers will differ in each run):
import cupy as cp
a = cp.random.normal(0, 1, 5 * 1024)
a
array([ 0.27293273, -1.77580853, 1.93887115, ..., -0.99303592,
-0.95136004, -0.38808653])
cp.sum(a.reshape(5, 1024), axis=1)
array([ 31.57886369, -17.67163523, 28.8791174 , -6.20866959,
-15.55492089])
import numba as nb
import numba.cuda
@nb.cuda.jit
def zero_out(array):
i = nb.cuda.grid(1)
array[i] = 0
zero_out[1024, 5](a)
a
array([0., 0., 0., ..., 0., 0., 0.])
Brief introduction to GPU programming#
A GPU is a device attached to a computer (usually separate from the main motherboard, through a PCI bus) that has its own memory and can perform calculations.
It differs from the CPUs in several ways. Whereas a typical computer has several CPUs that can all perform calculations independently in parallel, and has a hardware-managed CPU cache to speed up access to recently used data,
a GPU consists of thousands of independent processing units that can work in parallel,
with a much slower clock rate than a CPU,
small groups (32 or 64) of processing units aren’t independent; they have to perform the same instructions, but they can apply them to different data,
memory within the GPU is managed manually by the programmer.
In Seymour Cray’s metaphor, “If you were plowing a field, which would you rather use: two strong oxen or 1024 chickens?” a GPU is the thousand chickens. Certain types of problems are faster and more energy efficient to solve with a thousand chickens.
An algorithm intended for a CPU, like this:
void some_function(float* array, int index) {
array[index] = ...;
}
for (int i = 0; i < 1000000; i++) {
some_function(array, i);
}
would get translated into something like this for a GPU:
__global__ some_function(float* array) {
int index = blockIdx.x * blockDim.x + threadIdx.x;
array[index] = ...;
}
some_function<<<blocks_per_grid, threads_per_block>>>(array);
The explicit iteration over elements of an array (in sequential order) on the CPU is replaced by a GPU “kernel” function that applies to just one array element, and each kernel-execution “thread” might run at any time. The execution is organized into “blocks”: threads within a block run at the same time on shared resources, and the GPU schedules block execution in a way that keeps its streaming multiprocessors busy. The array must already be in the GPU’s global memory.
The blocks_per_grid and threads_per_block are units of work—they control how computations are scheduled on the GPU—not units of array allocation. However, for 1-dimensional data, it’s often best to define them in terms of the array size:
threads_per_block = 1024; // maximum possible on most GPUs
blocks_per_grid = int(ceil(1.0 * size_of_array / threads_per_block));
This minimizes the number of blocks needed to make sure that each array element is updated by exactly one thread.
If the size_of_array doesn’t fit neatly into an integer number of blocks, a few threads will be wasted. To make sure that they don’t update uninitialized data, you usually need to check for an excess in the kernel function:
__global__ some_function(float* array) {
int index = blockIdx.x * blockDim.x + threadIdx.x;
if (index < size_of_array) {
array[index] = ...;
}
}
We’ll see this with explicit examples in the next few sections.
CuPy#
CuPy is a library with mostly the same interface as NumPy, but all arrays are in GPU memory, rather than the motherboard’s RAM. Converting a NumPy array into a CuPy array, and vice-versa, copies data from RAM to GPU global memory and back.
import numpy as np
import cupy as cp
array_in_ram = np.random.uniform(0, 1, 100000000)
array_on_gpu = cp.asarray(array_in_ram)
%%timeit -r1 -n10
array_in_ram[:] += 1
60.9 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 10 loops each)
%%timeit -r1 -n10
array_on_gpu[:] += 1
2.15 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 10 loops each)
It’s important that the distinction is visible like this, since copying an array between RAM and the GPU is often more time-consuming than the computation itself.
%%timeit -r1 -n10
cp.asarray(array_in_ram) # from RAM to GPU
134 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 10 loops each)
%%timeit -r1 -n10
array_on_gpu.get() # from GPU to RAM
145 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 10 loops each)
Thus, you’ll want to keep the data on the device that is performing calculations for as long as possible. If data can be created on the GPU, such as random numbers for a Monte Carlo calculation, use CuPy’s functions to do it.
array_on_gpu = cp.random.uniform(0, 1, 100000000)
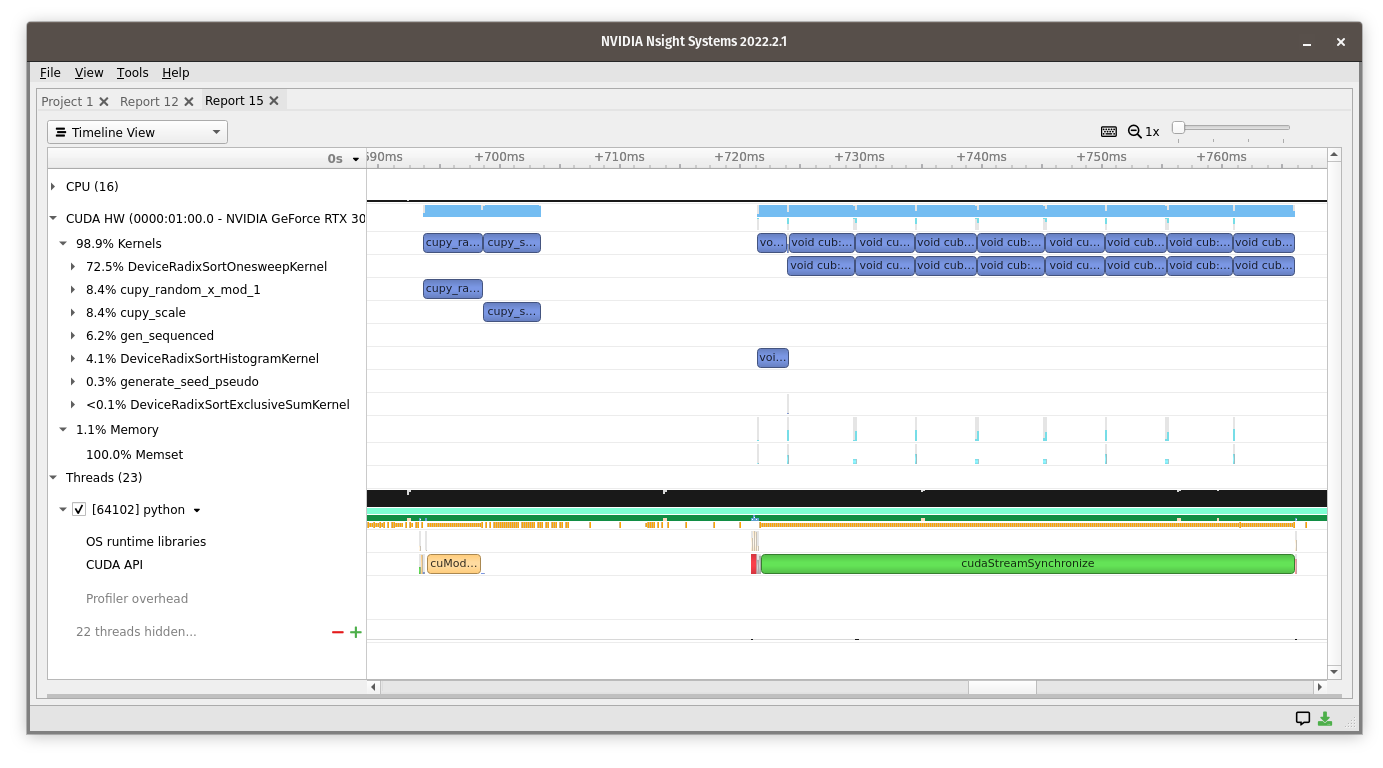
We can see more of what’s going on by running Nvidia’s nsys-ui profiler on the following line:
array = cp.random.uniform(5, 10, 100000000)
array.sort()
array
array([5. , 5.00000007, 5.0000002 , ..., 9.99999962, 9.99999966,
9.9999998 ])
The CUDA kernels (blue) from the first line runs
cupy_random_x_mod_1cupy_scale
to make the random numbers, followed by
DeviceRadixSortHistogramKernelDeviceRadixSortOnesweepKernel
to sort the random numbers. Meanwhile on the CPU (green), Python waits for the result with a
cudaStreamSynchronize
Since the GPU is a separate device from the CPU, it runs independently. If you don’t ask for the result, the Python function can finish while the GPU calculation is still running. It’s only when you want to print the result, copy it to a NumPy array, or get any element as a Python number that CuPy asks the GPU to “synchronize”—wait for computation to be finished.
Since the GPU runs independently, what should it do if it encounters an error part-way through processing? It can’t raise a Python error (the Python function call has already finished), so it has to do something else instead. CuPy defines some results that would be errors in NumPy. For instance, this array-slice asks for elements beyond the end of the array:
array = np.array([0.0, 1.1, 2.2, 3.3, 4.4, 5.5])
array[np.array([2, 3, 5, 6, 7, 8])]
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
Cell In[17], line 3
1 array = np.array([0.0, 1.1, 2.2, 3.3, 4.4, 5.5])
----> 3 array[np.array([2, 3, 5, 6, 7, 8])]
IndexError: index 6 is out of bounds for axis 0 with size 6
But CuPy returns a result by wrapping the indexes around to the beginning of the array (6 → 0, 7 → 1, 8 → 2):
array = cp.array([0.0, 1.1, 2.2, 3.3, 4.4, 5.5])
array[cp.array([2, 3, 5, 6, 7, 8])]
array([2.2, 3.3, 5.5, 0. , 1.1, 2.2])
So you may need to check the correctness of your code in NumPy before running it at high speed in CuPy.
Next, we should note that just replacing NumPy with CuPy has the same shortcoming as array-oriented Python versus compiled code: although it’s a first (easy) step toward speeding up a computation, it’s not the fastest possible because intermediate arrays have to be allocated in each step.
Remember how the quadratic formula
a = cp.random.uniform(5, 10, 1000000)
b = cp.random.uniform(10, 20, 1000000)
c = cp.random.uniform(-0.1, 0.1, 1000000)
(-b + cp.sqrt(b**2 - 4*a*c)) / (2*a)
array([ 0.00354629, 0.00108686, -0.0014943 , ..., 0.00375009,
0.00123045, -0.00259124])
is roughly equivalent to
tmp1 = cp.negative(b) # -b
tmp2 = cp.square(b) # b**2
tmp3 = cp.multiply(4, a) # 4*a
tmp4 = cp.multiply(tmp3, c) # tmp3*c
del tmp3
tmp5 = cp.subtract(tmp2, tmp4) # tmp2 - tmp4
del tmp2, tmp4
tmp6 = cp.sqrt(tmp5) # sqrt(tmp5)
del tmp5
tmp7 = cp.add(tmp1, tmp6) # tmp1 + tmp6
del tmp1, tmp6
tmp8 = cp.multiply(2, a) # 2*a
np.divide(tmp7, tmp8) # tmp7 / tmp8
array([ 0.00354629, 0.00108686, -0.0014943 , ..., 0.00375009,
0.00123045, -0.00259124])
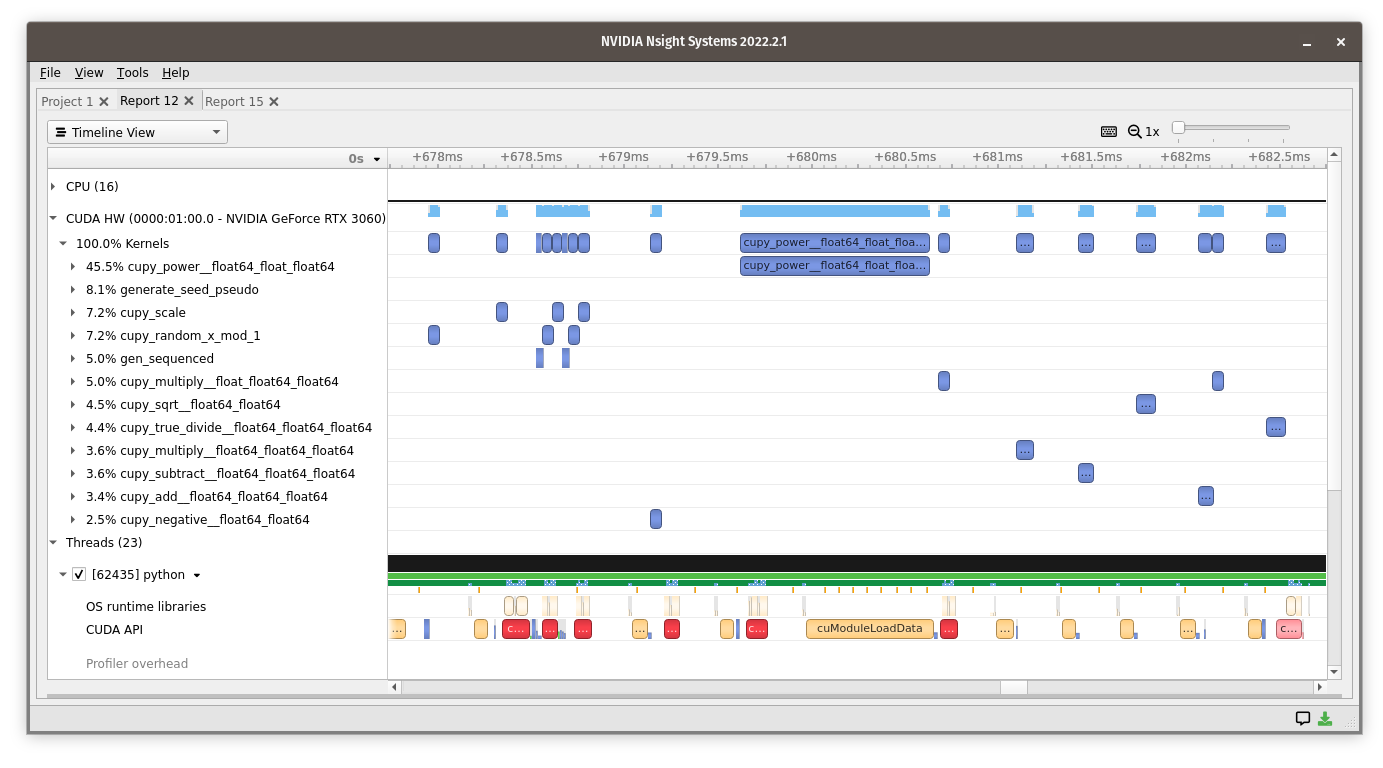
Here’s what that looks like in the profiler:
Each of the
cupy_power__float64_float_float64cupy_multiply__float_float64_float64cupy_sqrt__float64_float64cupy_true_divide__float64_float64_float64cupy_multiply__float64_float64_float64cupy_subtract__float64_float64_float64cupy_add__float64_float64_float64cupy_negative__float64_float64
kernels runs quickly, but there are time-gaps between them in which arrays are allocated and dynamic code decides what to do next. It would be faster if the whole quadratic formula were “fused” into a single kernel.
To support this, CuPy has a JIT compiler that lets you write C++ CUDA code. For instance, the worst part of the calculation above is using a general floating-point power function,
cupy_power__float64_float_float64
to compute power(b, 2), which should be just b * b. Let’s define a better function for “raising to an integer power”.
intpow = cp.ElementwiseKernel("float64 x, int64 n", "float64 out", '''
out = 1.0;
for (int i = 0; i < n; i++) {
out *= x;
}
''', "intpow")
intpow
<cupy._core._kernel.ElementwiseKernel at 0x7228e4267060>
intpow(b, 2)
array([349.69803979, 119.27597606, 300.9489732 , ..., 227.78363405,
235.76110542, 178.84017007])
b**2
array([349.69803979, 119.27597606, 300.9489732 , ..., 227.78363405,
235.76110542, 178.84017007])
We can also do this with the whole quadratic formula.
quadratic_formula = cp.ElementwiseKernel("float64 a, float64 b, float64 c", "float64 out", '''
out = (-b + sqrt(b*b - 4*a*c)) / (2*a);
''', "quadratic_formula")
quadratic_formula(a, b, c)
array([ 0.00354629, 0.00108686, -0.0014943 , ..., 0.00375009,
0.00123045, -0.00259124])
%%timeit -r1 -n1000
(-b + cp.sqrt(b**2 - 4*a*c)) / (2*a)
1.34 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1,000 loops each)
%%timeit -r1 -n1000
quadratic_formula(a, b, c)
163 μs ± 0 ns per loop (mean ± std. dev. of 1 run, 1,000 loops each)
Both of the above used ElementwiseKernel, which is like a NumPy ufunc: they take arrays and apply the function to each element. We could also write a fully generic RawKernel, but then we’d have to manage the threads_per_block and blocks_per_grid manually.
quadratic_formula_raw = cp.RawKernel(r'''
extern "C" __global__
void quadratic_formula_raw(const double* a, const double* b, const double* c, int length, double* out) {
int i = blockDim.x * blockIdx.x + threadIdx.x;
if (i < length) {
out[i] = (-b[i] + sqrt(b[i]*b[i] - 4*a[i]*c[i])) / (2*a[i]);
}
}
''', "quadratic_formula_raw")
out = cp.empty_like(a)
threads_per_block = 1024
blocks_per_grid = int(np.ceil(len(out) / 1024))
quadratic_formula_raw((blocks_per_grid,), (threads_per_block,), (a, b, c, len(out), out))
out
array([ 0.00354629, 0.00108686, -0.0014943 , ..., 0.00375009,
0.00123045, -0.00259124])
Thus, CuPy is two things:
an array library with the NumPy interface, but all arrays are on GPUs,
a JIT compiler of CUDA kernels written in C++.
This situation is similar to writing custom C++ code with pybind11, rather than writing the kernel in Python.
Numba#
Just as Numba can JIT compile Python for CPUs, it can JIT compile Python to CUDA.
Here’s the quadratic formula as a single CUDA kernel without writing any C++.
import numba.cuda # must be explicitly imported
import math # note that Numba-CUDA requires math.*; you can't use np.*
@nb.cuda.jit
def quadratic_formula_numba_cuda(a, b, c, out):
i = nb.cuda.grid(1) # 1-dimensional
if i < len(out):
out[i] = (-b[i] + math.sqrt(b[i]**2 - 4*a[i]*c[i])) / (2*a[i])
out = cp.empty_like(a)
threads_per_block = 1024
blocks_per_grid = int(np.ceil(len(out) / 1024))
quadratic_formula_numba_cuda[blocks_per_grid, threads_per_block](a, b, c, out)
out
array([ 0.00354629, 0.00108686, -0.0014943 , ..., 0.00375009,
0.00123045, -0.00259124])
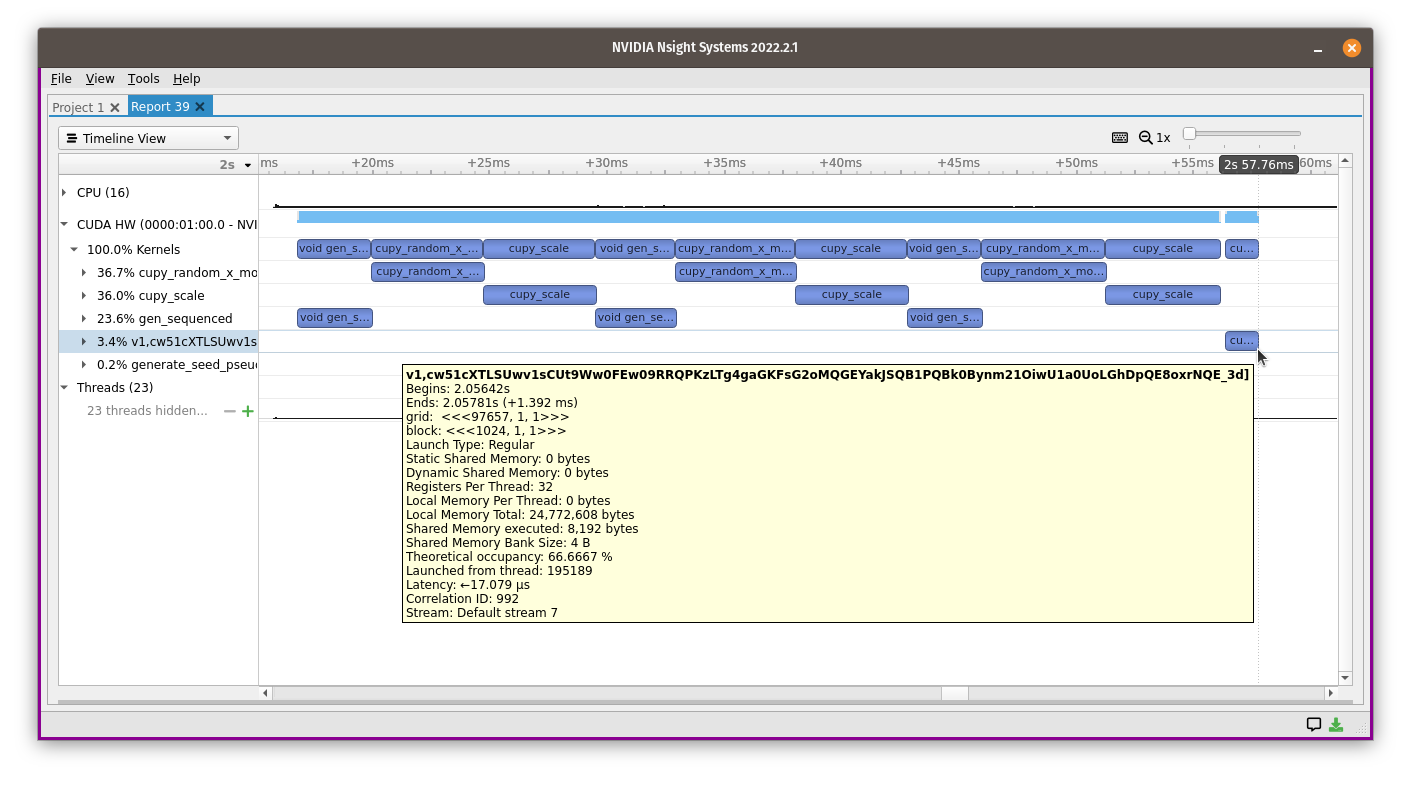
Here’s what it looks like in the profiler:
The name is a long random string, but it all runs in a short block of time.
Note that the structure of a @nb.cuda.jit compiled function is equivalent to a C++ CUDA function: all that has changed is the Python syntax and the names of some of the functions:
extern "C" __global__
void quadratic_formula_raw(const double* a, const double* b, const double* c, int length, double* out) {
int i = blockDim.x * blockIdx.x + threadIdx.x;
if (i < length) {
out[i] = (-b[i] + sqrt(b[i]*b[i] - 4*a[i]*c[i])) / (2*a[i]);
}
}
quadratic_formula_raw<<<blocks_per_grid, threads_per_block>>>(a, b, c, size_of_array, out);
versus
@nb.cuda.jit
def quadratic_formula_numba_cuda(a, b, c, out):
i = nb.cuda.grid(1) # 1-dimensional
if i < len(out):
out[i] = (-b[i] + math.sqrt(b[i]**2 - 4*a[i]*c[i])) / (2*a[i])
quadratic_formula_numba_cuda[blocks_per_grid, threads_per_block](a, b, c, out)
You still have to choose an optimal blocks_per_grid and threads_per_block, and the kernel gets its thread index through a special function, nb.cuda.grid.
JAX#
Just as JAX inspects array-oriented code, identifies which functions can be fused, and JIT compiles the fused kernel for the CPU, it can do the same for GPUs. In fact, a JAX array has a device parameter that determines whether it will be in RAM or on the GPU.
Instead of performing the same demonstration with the quadratic formula, see mandelbrot-on-all-accelerators.ipynb in your notebooks folder. It takes a single calculation, which draws the Mandelbrot set, and accelerates it using all of the techniques we’ve discussed, including CuPy’s RawKernel, Numba-CUDA, and JAX-CUDA. Here’s the bottom line:
Custom CUDA kernels are the fastest, regardless of whether they are compiled by CuPy, Numba, or JAX.
Awkward Array#
Awkward Arrays can be copied to a GPU using ak.to_backend with backend="cuda".
import awkward as ak
import uproot
with uproot.open("data/SMHiggsToZZTo4L.root:Events") as tree:
events_pt, events_eta, events_phi, events_charge = tree.arrays(
["Electron_pt", "Electron_eta", "Electron_phi", "Electron_charge"], how=tuple
)
electrons = ak.to_backend(
ak.zip({
"pt": events_pt,
"eta": events_eta,
"phi": events_phi,
"charge": events_charge,
},
with_name="Momentum4D",
), "cuda")
electrons
[[],
[{pt: 21.90268, eta: -0.7021887, phi: 0.13399617, charge: 1}, ..., {...}],
[{pt: 11.571167, eta: -0.8493275, phi: 2.1804526, charge: -1}, {...}],
[{pt: 10.413637, eta: -0.022762615, phi: -0.64317286, charge: -1}],
[{pt: 30.733414, eta: -0.610117, phi: 1.0087388, charge: -1}, ..., {...}],
[{pt: 16.080765, eta: 0.34038106, phi: -0.4972907, charge: 1}],
[{pt: 5.3183117, eta: -0.5736427, phi: -1.4705021, charge: -1}],
[{pt: 6.988549, eta: 0.52973014, phi: -0.6329002, charge: 1}],
[{pt: 40.959602, eta: -0.21598065, phi: 2.7890391, charge: -1}, ..., {...}],
[],
...,
[{pt: 19.12917, eta: 1.1267458, phi: -0.4354926, charge: -1}, {...}],
[{pt: 30.197298, eta: 1.8354917, phi: 1.9399015, charge: 1}],
[],
[{pt: 37.00934, eta: -2.3536925, phi: 0.9030401, charge: 1}, ..., {...}],
[],
[{pt: 12.313824, eta: -0.27283365, phi: -3.108863, charge: 1}],
[],
[{pt: 17.923506, eta: 2.2025933, phi: -1.1234515, charge: -1}, {...}],
[{pt: 48.07147, eta: 0.53210974, phi: -1.6076394, charge: -1}, {...}]]
---------------------------------------------------------------------------------------------------------
backend: cuda
nbytes: 9.2 MB
type: 299973 * var * Momentum4D[
pt: float32,
eta: float32,
phi: float32,
charge: int32
]With this backend, all mathematical computations are performed by CuPy (directly or through JIT compiled functions).
Below is a calculation of the mass of the heaviest dielectron in each event, using
for the invariant mass.
e1, e2 = ak.unzip(ak.combinations(electrons, 2))
z_mass = np.sqrt(
2*e1.pt*e2.pt * (np.cosh(e1.eta - e2.eta) - np.cos(e1.phi - e2.phi))
)
np.max(z_mass, axis=-1)
[None, 76.752525, 36.007294, None, 87.34057, None, None, None, 92.22189, None, ..., 27.277554, None, None, 107.22261, None, None, None, 40.64742, 91.51784] ----------------------- backend: cuda nbytes: 1.5 MB type: 299973 * ?float32
GPU-bound Awkward Arrays can also be iterated over in Numba-CUDA, which allows for imperative code. However, the output must be a non-ragged CuPy array.
ak.numba.register_and_check()
@nb.cuda.jit(extensions=[ak.numba.cuda])
def mass_of_heaviest_dielectron(electrons, out):
thread_idx = nb.cuda.grid(1)
if thread_idx < len(electrons):
electrons_in_one_event = electrons[thread_idx]
for i, e1 in enumerate(electrons_in_one_event):
for e2 in electrons_in_one_event[i + 1:]:
if e1.charge != e2.charge:
m = math.sqrt(
2*e1.pt*e2.pt * (math.cosh(e1.eta - e2.eta) - math.cos(e1.phi - e2.phi))
)
if m > out[thread_idx]:
out[thread_idx] = m
threads_per_block = 1024
blocks_per_grid = int(np.ceil(len(electrons) / 1024))
out = cp.zeros(len(electrons), dtype=np.float32)
mass_of_heaviest_dielectron[blocks_per_grid, threads_per_block](electrons, out)
out
array([ 0. , 76.752525, 36.007294, ..., 0. , 40.647415,
91.51784 ], dtype=float32)
To make this a little more readable, let’s rewrite it as a __device__ function, which is a function that has a return value (doesn’t have to overwrite an array) but can only be called from GPU-bound functions.
@nb.cuda.jit(extensions=[ak.numba.cuda], device=True)
def compute_mass(event):
out = np.float32(0)
for i, e1 in enumerate(event):
for e2 in event[i + 1:]:
if e1.charge != e2.charge:
m = math.sqrt(
2*e1.pt*e2.pt * (math.cosh(e1.eta - e2.eta) - math.cos(e1.phi - e2.phi))
)
if m > out:
out = m
return out
@nb.cuda.jit(extensions=[ak.numba.cuda])
def mass_of_heaviest_dielectron_2(events, out):
thread_idx = nb.cuda.grid(1)
if thread_idx < len(events):
out[thread_idx] = compute_mass(events[thread_idx])
# same threads_per_block, blocks_per_grid
out = cp.zeros(len(electrons), dtype=np.float32)
mass_of_heaviest_dielectron_2[blocks_per_grid, threads_per_block](electrons, out)
out
array([ 0. , 76.752525, 36.007294, ..., 0. , 40.647415,
91.51784 ], dtype=float32)
Lesson 5 project: Histograms and Monte Carlo on GPUs#
As described in the intro, navigate to the notebooks directory and open lesson-5-project.ipynb, then follow its instructions.