Lesson 1: The Python language

Lesson 1: The Python language#

If you’re following this course, you’re probably already familiar with the Python programming language—at least a little bit. Nevertheless, I’ll start with a review of the language for three reasons:

  • to make sure there aren’t any gaps in your knowledge,

  • so that you can be confident that there isn’t something extra you need to know,

  • array-oriented programming emphasizes a different subset of the language, as you’ll see.

On the last point, this review of Python covers for and if statements last, rather than first, and doesn’t cover classes. Defining classes is an important part of Python programming, but we won’t be using it.

Why Python?#

Python is now the most popular programming language for many applications. For our purposes, what’s relevant is that it is the most popular language for data analysis. Below are plots of search volume from Google Trends that show how often people search for “data analysis” and “machine learning” in the same query with “Python”, “R”, and “Java”.

“Popularity” means more tools are available, more attention has been drawn to their shortcomings, and you can find more information about how to use them online. It also means that Python skills are transferable skills.

Python as an interactive calculator#

The most important thing about Python, especially for data analysis, is that it is an interactive language. Unlike “compile-first” languages such as C++, Fortran, and Rust, you can partially run a program and type arbitrary commands into a terminal or a Jupyter notebook, while it runs.

The cost of this interactivity is speed. Python has a severe performance penalty compared to “compile-first” languages, so if you’re not using this interactivity (for instance, by always running whole scripts at a time), you’re missing out on a feature you’re paying for!

Any expression typed on the Python prompt or in a Jupyter cell computes the expression and returns the result:

2 + 2

4

You can also define variables,

E = 68.1289790
px = -17.945541
py = 13.1652603
pz = 64.3908386

and use them in expressions.

For instance, calculate \({p_x}^2 + {p_y}^2\).

px**2 + py**2

495.36652054943704

Now the transverse momentum \(p_T = \sqrt{{p_x}^2 + {p_y}^2 + {p_z}^2}\).

(px**2 + py**2 + pz**2)**(1/2)

68.12889707136529

The examples in this introduction to Python are inspired by particle physics, so we’ll be using the momentum-energy relations a lot:

\[p = \sqrt{{p_x}^2 + {p_y}^2 + {p_z}^2}\]
\[m = \sqrt{E^2 - p^2}\]

Mini-quiz 1: Fix the mistake!

m = (E**2 - px**2 + py**2 + pz**2)**(1/2)
m

92.94632597460625

(The result above is wrong.)

For reference, here’s a table of Python’s arithmetic operators:

operator

meaning

returns

x + y

addition

same type of number

x - y

subtraction

same type of number

-x

negation

same type of number

x * y

multiplication

same type of number

x / y

division

floating-point number

x // y

truncated division

integer number

x % y

modulo (remainder)

integer number

x ** y

exponentiation

same type of number

x == y

equality

boolean (True or False)

x != y

inequality

boolean (True or False)

x < y

less than

boolean (True or False)

x <= y

less than or equal to

boolean (True or False)

x > y

greater than

boolean (True or False)

x >= y

greater than or equal to

boolean (True or False)

x @ y

matrix multiplication

array

~x

bitwise not

integer number

x & y

bitwise and

integer number

x | y

bitwise or

integer number

x ^ y

bitwise xor

integer number

Defining functions#

The syntax for defining a function is:

def euclidean(x, y, z):
    return (x**2 + y**2 + z**2)**(1/2)

def minkowski(time, space):
    return (time**2 - space**2)**(1/2)

We can call them using arguments identified by position,

euclidean(px, py, pz)

68.12889707136529

or by name,

euclidean(z=pz, y=py, x=px)

68.12889707136529

The arguments of a function call can be the return values of other functions.

minkowski(E, euclidean(px, py, pz))

0.10565709515008793

You can also define functions inside of functions.

def mass(E, px, py, pz):
    def euclidean(x, y, z):
        return (x**2 + y**2 + z**2)**(1 / 2)

    def minkowski(time, space):
        return (time**2 - space**2)**(1 / 2)

    return minkowski(E, euclidean(px, py, pz))

mass(E, px, py, pz)

0.10565709515008793

Note that the nesting is indicated by indenting, rather than curly brackets ({ }), an end token, or any other syntax. The rules are:

  • the first statement must have no whitespace (no tabs or spaces),

  • nesting is opened by increasing the whitespace relative to the previous line,

  • nesting is closed by decreasing the whitespace to a previously established level.

“Whitespace” can be tabs or spaces, but since both are invisible, it can be easy to confuse them. Most codebases use a standard of 4 spaces (and never use tabs), which is what we’ll do here.

Functions are objects#

The functions that we defined above are objects that can be referred to by variables, just like numbers.

mag3d = euclidean

Now mag3d can be used in exactly the same ways as euclidean, because they’re just two names for the same thing.

mag3d(px, py, pz)

68.12889707136529

Python’s is keyword tells you whether two varible names refer to the same object (as opposed to just being equal to the same value).

mag3d is euclidean

True

In fact, we’re free to delete (del) the original and keep using it with the new name.

euclidean(px, py, pz)

68.12889707136529

mag3d(px, py, pz)

68.12889707136529

del euclidean

mag3d(px, py, pz)

68.12889707136529

We can think of the def syntax as doing two things:

  1. defining the function,

  2. assigning it to a variable name.

Importing functions into Python#

One of the reasons to prefer a popular language like Python is that much of the functionality you need already exists as free software. You can just install the packages you need, import them into your session, and then use them.

It’s important to understand the distinction between

  • installing: downloading the packages onto the computer you’re using (with pip, conda, uv, pixi, …), so that they become available as modules

  • importing: assigning variable names to the functions in those modules

Python comes with some modules built into its standard library. If you have Python, these modules are already installed.

One of these pre-installed modules is called math.

import math

The above statement has assigned the module as a new variable name, math.

math

<module 'math' from '/home/runner/micromamba/envs/array-oriented-programming/lib/python3.11/lib-dynload/math.cpython-311-x86_64-linux-gnu.so'>

You can access functions in the module with a dot (.).

math.sqrt

<function math.sqrt(x, /)>

We can now use math.sqrt instead of **(1/2).

math.sqrt(E**2 - px**2 - py**2 - pz**2)

0.10565709514578395

NumPy is a package that needs to be installed before you can use it. (In the intro, I described a few different ways to install it.)

import numpy

numpy

<module 'numpy' from '/home/runner/micromamba/envs/array-oriented-programming/lib/python3.11/site-packages/numpy/__init__.py'>

The NumPy package also defines a function called sqrt. The dot-syntax ensures that they can be distinguished.

numpy.sqrt(E**2 - px**2 - py**2 - pz**2)

np.float64(0.10565709514578395)

math.sqrt is numpy.sqrt

False

The variable name that you use for the module doesn’t have to be the same as its package name. In fact, some packages have conventional “short names” that they encourage you to use.

import numpy as np

numpy is np

True

del numpy

np.sqrt(E**2 - px**2 - py**2 - pz**2)

np.float64(0.10565709514578395)

Sometimes, you’ll want to extract only one or a few objects from a module, but not assign the module itself to a variable name.

from hepunits import GeV
from particle import Particle

muon = Particle.from_name("mu+")
muon
\[\mu^{+}\]
muon.mass / GeV

0.1056583755

Data types#

Python has data types, but unlike “compile-first” languages, it only verifies whether you’re using the types correctly right before a computation, rather than in a compilation phase.

1 + "2"

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[33], line 1
----> 1 1 + "2"

TypeError: unsupported operand type(s) for +: 'int' and 'str'

You can determine an object’s type with the type function.

type(1)

int

type("2")

str

type(True)

bool

type(False)

bool

Also unlike “compile-first” languages, these types are objects that can be assigned to variables, like any other object.

t1 = type(1)
t2 = type("2")

t1

int

t2

str

Most type objects are also functions that create or convert data to that type.

int("2")

2

t1("2")

2

Mini-quiz 2: Before you run the following, what will it do?

Hint: break it down in parts and test each part.

type(type(1)("2"))

Type hierarchies#

Types are like sets: the number 1 is a member of the set int, and the string "2" is a member of the set str. Sets can have subsets, such as “whole numbers are a subset of real numbers.”

Let’s see this using NumPy’s numeric types. np.int32 is a type (and constructor of) integers using 32 bits of memory.

np.int32(1)

np.int32(1)

np_one = np.int32(1)

type(np_one)

numpy.int32

type(np_one) is np.int32

True

This 32-bit integer type is a subtype of np.integer, which we can see by asking if 32-bit integer instances are instances of np.integer,

isinstance(np_one, np.integer)

True

or by asking if the np.int32 type is a subtype (“subclass”) of np.integer.

issubclass(np.int32, np.integer)

True

NumPy has a large hierarchy of subtypes within supertypes, which is independent of the Python number hierarchy.

Notice that NumPy and Python have different opinions about whether booleans are integers.

Mini-quiz 3: Write two expressions to show that booleans in Python are integers and booleans in NumPy are not.

Collection types#

Collections are Python objects that contain objects. The two most basic collection types in Python are list and dict.

some_list = [0.0, 1.1, 2.2, 3.3, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9]
some_list

[0.0, 1.1, 2.2, 3.3, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9]

type(some_list)

list

len(some_list)

10

some_dict = {"one": 1.1, "two": 2.2, "three": 3.3}
some_dict

{'one': 1.1, 'two': 2.2, 'three': 3.3}

type(some_dict)

dict

len(some_dict)

3

You can get an object out of a list or dict using square brackets ([ ]).

some_list[3]

3.3

some_dict["two"]

2.2

You can also change the data in a collection if the square brackets are on the left of an assignment (=).

some_list[3] = 33333

some_list

[0.0, 1.1, 2.2, 33333, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9]

some_dict["two"] = 22222

some_dict

{'one': 1.1, 'two': 22222, 'three': 3.3}

And you can extend them beyond their original length, as well as mix different data types in the same collection.

some_list.append("mixed types")

some_list

[0.0, 1.1, 2.2, 33333, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9, 'mixed types']

some_dict[123] = "mixed types"

some_dict

{'one': 1.1, 'two': 22222, 'three': 3.3, 123: 'mixed types'}

Ranges within a list can be “sliced” with a colon (:).

some_list[2:8]

[2.2, 33333, 4.4, 5.5, 6.6, 7.7]

Mini-quiz 4: Before you run it, what will the following do?

some_list[2:8][3]

(We’ll see more about slices in the next lesson on arrays.)

One last thing: some_list.append, above, is our example of a method. A method is just a function on a data object, accessed through the dot (.) operator. It’s very similar to a function in a module.

dict objects have three very useful methods: keys, values, and items.

some_dict.keys()

dict_keys(['one', 'two', 'three', 123])

some_dict.values()

dict_values([1.1, 22222, 3.3, 'mixed types'])

some_dict.items()

dict_items([('one', 1.1), ('two', 22222), ('three', 3.3), (123, 'mixed types')])

A little data analysis#

Now let’s use Python collections to perform some steps in a data analysis. Suppose you have this (small!) collection of observed particles,

particles = [
    {"type": "electron", "E": 171.848714, "px": 38.4242935, "py": -28.779644, "pz": 165.006927, "charge": 1,},
    {"type": "electron", "E": 138.501266, "px": -34.431419, "py": 24.6730384, "pz": 131.864776, "charge": -1,},
    {"type": "muon", "E": 68.1289790, "px": -17.945541, "py": 13.1652603, "pz": 64.3908386, "charge": 1,},
    {"type": "muon", "E": 18.8320473, "px": -8.1843795, "py": -7.6400470, "pz": 15.1420097, "charge": -1,},
]

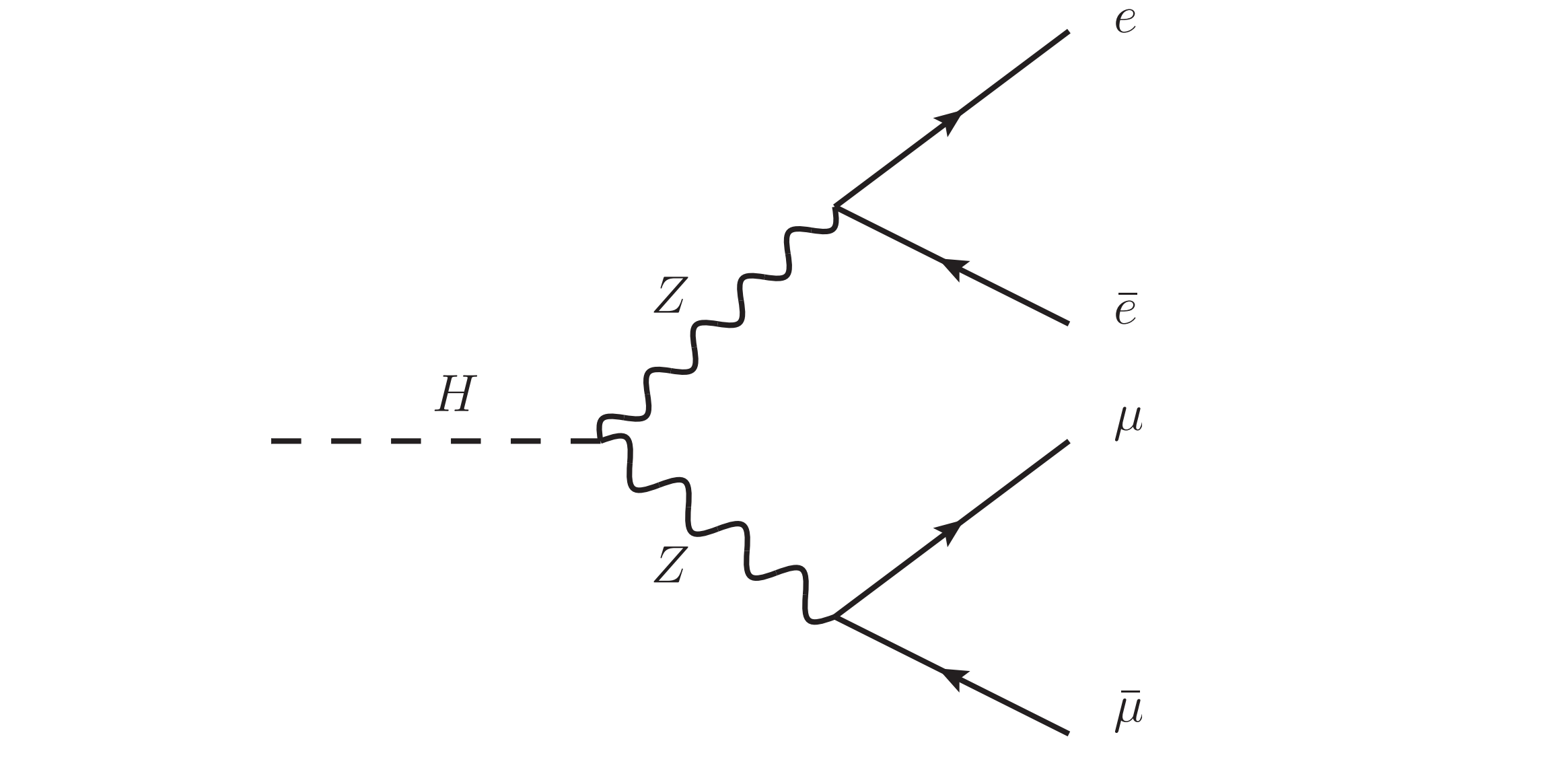
and you want to infer the energy and momentum of the Higgs and Z bosons that decayed into electrons and muons through this mechanism:

A particle that decays into particle1 and particle2 has the sum of energy, momentum, and charge of these observed particles, so let’s make a helper function for that.

def particle_decay(name, particle1, particle2):
    return {
        "type": name,
        "E": particle1["E"] + particle2["E"],
        "px": particle1["px"] + particle2["px"],
        "py": particle1["py"] + particle2["py"],
        "pz": particle1["pz"] + particle2["pz"],
        "charge": particle1["charge"] + particle2["charge"],
    }

Let’s call the Z that decayed into electrons z1,

z1 = particle_decay("Z boson", particles[0], particles[1])
z1

{'type': 'Z boson',
 'E': 310.34997999999996,
 'px': 3.992874499999999,
 'py': -4.106605600000002,
 'pz': 296.871703,
 'charge': 0}

and the Z that decayed into muons z2,

z2 = particle_decay("Z boson", particles[2], particles[3])
z2

{'type': 'Z boson',
 'E': 86.9610263,
 'px': -26.129920499999997,
 'py': 5.5252133,
 'pz': 79.5328483,
 'charge': 0}

The Higgs boson decayed into the two Z bosons, so we can compute its energy and momentum using z1 and z2 as input.

higgs = particle_decay("Higgs boson", z1, z2)
higgs

{'type': 'Higgs boson',
 'E': 397.3110063,
 'px': -22.137045999999998,
 'py': 1.4186076999999981,
 'pz': 376.40455130000004,
 'charge': 0}

Mini-quiz 5: Define a particle_mass function using an equation given earlier in this lesson and use it to compute the masses of z1, z2, and higgs.

def particle_mass(particle):
    ...

for loops and if branches#

Can you believe we got this far without for and if?

These are the fundamental building blocks of imperative programming, but our focus will be on array-oriented programming.

for is used to repeat Python statements. Python runs one statement at a time, and the statements in an indented for block are run zero or more times.

for particle in particles:
    print(particle["type"], particle["charge"])

electron 1
electron -1
muon 1
muon -1

It doesn’t even look ahead to see if there’s trouble coming on the next line.

for particle in particles:
    print(particle["type"])
    print(particle["charge"])
    print(particle["something it does not have"])

electron
1

---------------------------------------------------------------------------
KeyError                                  Traceback (most recent call last)
Cell In[76], line 4
      2 print(particle["type"])
      3 print(particle["charge"])
----> 4 print(particle["something it does not have"])

KeyError: 'something it does not have'

if tells it whether it should enter an indented block or not, depending on whether an expression is True or False.

for particle in particles:
    if particle["type"] == "electron":
        print(particle)

{'type': 'electron', 'E': 171.848714, 'px': 38.4242935, 'py': -28.779644, 'pz': 165.006927, 'charge': 1}
{'type': 'electron', 'E': 138.501266, 'px': -34.431419, 'py': 24.6730384, 'pz': 131.864776, 'charge': -1}

It can switch between two indented blocks if an else clause is given.

for particle in particles:
    if particle["type"] == "electron":
        print(particle)
    else:
        print("not an electron")

{'type': 'electron', 'E': 171.848714, 'px': 38.4242935, 'py': -28.779644, 'pz': 165.006927, 'charge': 1}
{'type': 'electron', 'E': 138.501266, 'px': -34.431419, 'py': 24.6730384, 'pz': 131.864776, 'charge': -1}
not an electron
not an electron

if (and for) statements can be nested.

for particle in particles:
    if particle["type"] == "electron":
        if particle["charge"] > 0:
            print("e+")
        else:
            print("e-")
    else:
        if particle["charge"] > 0:
            print("mu+")
        else:
            print("mu-")

e+
e-
mu+
mu-

And elif works as a contraction of else if with less indenting.

for particle in particles:
    if particle["type"] == "electron" and particle["charge"] > 0:
        print("e+")
    elif particle["type"] == "electron" and particle["charge"] < 0:
        print("e-")
    elif particle["type"] == "muon" and particle["charge"] > 0:
        print("mu+")
    elif particle["type"] == "muon" and particle["charge"] < 0:
        print("mu-")

e+
e-
mu+
mu-

List and dict comprehensions#

Python has some syntax features to make code faster to type. I’m avoiding most of these, but I need to introduce “comprehensions” because I use them later in the course. The “comprehension” syntax uses for inside of a list or dict constructor as a shortcut for building collections.

Starting from an existing collection, like

original_list = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

The basic way to make a new list of squared values is

new_list = []
for x in original_list:
    new_list.append(x**2)

new_list

[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]

But the for loop can be written inside of the new_list constructor.

new_list = [x**2 for x in original_list]
new_list

[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]

This is a “list comprehension”. A similar constructor, using curly brackets ({ }) and a colon (:) makes dicts. It’s called a “dict comprehension”.

new_dict = {str(x): x**2 for x in original_list}
new_dict

{'1': 1,
 '2': 4,
 '3': 9,
 '4': 16,
 '5': 25,
 '6': 36,
 '7': 49,
 '8': 64,
 '9': 81,
 '10': 100}

It’s often convenient to use dict.items with a dict comprehension, since for loops only iterate over the keys.

{k: np.sqrt(v) for k, v in new_dict.items()}

{'1': np.float64(1.0),
 '2': np.float64(2.0),
 '3': np.float64(3.0),
 '4': np.float64(4.0),
 '5': np.float64(5.0),
 '6': np.float64(6.0),
 '7': np.float64(7.0),
 '8': np.float64(8.0),
 '9': np.float64(9.0),
 '10': np.float64(10.0)}

You can also use if at the end of the list or dict comprehension to skip over elements.

[x for x in original_list if x % 2 == 0]

[2, 4, 6, 8, 10]

A larger dataset#

import json

dataset = json.load(open("data/SMHiggsToZZTo4L.json"))

type(dataset)

list

len(dataset)

10000

Show just the first 3 collision events using a slice, 0:3.

dataset[0:3]

[{'run': 1,
  'luminosityBlock': 156,
  'event': 46501,
  'PV': {'x': 0.24369880557060242,
   'y': 0.3936990201473236,
   'z': 1.451307773590088},
  'electron': [],
  'muon': [{'pt': 63.04386901855469,
    'eta': -0.7186822295188904,
    'phi': 2.968005895614624,
    'mass': 0.10565836727619171,
    'charge': 1,
    'pfRelIso03_all': 0.0,
    'pfRelIso04_all': 0.0,
    'dxy': -0.004785160068422556,
    'dxyErr': 0.0060764215886592865,
    'dz': 0.09005985409021378,
    'dzErr': 0.044572051614522934},
   {'pt': 38.12034606933594,
    'eta': -0.8794569969177246,
    'phi': -1.0324749946594238,
    'mass': 0.10565836727619171,
    'charge': -1,
    'pfRelIso03_all': 0.0,
    'pfRelIso04_all': 0.0,
    'dxy': 0.0005746808601543307,
    'dxyErr': 0.0013040687190368772,
    'dz': -0.0032290113158524036,
    'dzErr': 0.003023269586265087},
   {'pt': 4.04868745803833,
    'eta': -0.320764422416687,
    'phi': 1.0385035276412964,
    'mass': 0.10565836727619171,
    'charge': 1,
    'pfRelIso03_all': 0.0,
    'pfRelIso04_all': 0.17997965216636658,
    'dxy': -0.00232272082939744,
    'dxyErr': 0.004343290813267231,
    'dz': -0.005162843037396669,
    'dzErr': 0.004190043080598116}],
  'MET': {'pt': 21.929929733276367, 'phi': -2.7301223278045654}},
 {'run': 1,
  'luminosityBlock': 156,
  'event': 46502,
  'PV': {'x': 0.24427825212478638,
   'y': 0.3952622413635254,
   'z': -2.879779100418091},
  'electron': [{'pt': 21.902679443359375,
    'eta': -0.7021886706352234,
    'phi': 0.1339961737394333,
    'mass': 0.00543835386633873,
    'charge': 1,
    'pfRelIso03_all': 0.15310849249362946,
    'dxy': -0.0005134913371875882,
    'dxyErr': 0.002374568721279502,
    'dz': -0.003061089664697647,
    'dzErr': 0.0025612758472561836},
   {'pt': 42.63296890258789,
    'eta': -0.9796805381774902,
    'phi': -1.8634047508239746,
    'mass': 0.008667422458529472,
    'charge': 1,
    'pfRelIso03_all': 0.07332895696163177,
    'dxy': 0.0016475901938974857,
    'dxyErr': 0.0029195048846304417,
    'dz': 0.0027775841299444437,
    'dzErr': 0.003392990678548813},
   {'pt': 78.01239013671875,
    'eta': -0.9338527917861938,
    'phi': -2.2078325748443604,
    'mass': 0.018527036532759666,
    'charge': -1,
    'pfRelIso03_all': 0.02972797304391861,
    'dxy': -0.0011600104626268148,
    'dxyErr': 0.0025206799618899822,
    'dz': 0.002125623868778348,
    'dzErr': 0.003055028384551406},
   {'pt': 23.835430145263672,
    'eta': -1.362490177154541,
    'phi': -0.6215649247169495,
    'mass': 0.008162532933056355,
    'charge': -1,
    'pfRelIso03_all': 0.074398934841156,
    'dxy': -0.0017699336167424917,
    'dxyErr': 0.005515107419341803,
    'dz': 0.0029383390210568905,
    'dzErr': 0.004372752271592617}],
  'muon': [],
  'MET': {'pt': 16.97213363647461, 'phi': 2.866946220397949}},
 {'run': 1,
  'luminosityBlock': 156,
  'event': 46503,
  'PV': {'x': 0.24243676662445068,
   'y': 0.39509689807891846,
   'z': 1.8682630062103271},
  'electron': [{'pt': 11.5711669921875,
    'eta': -0.8493275046348572,
    'phi': 2.180452585220337,
    'mass': -0.00608546519652009,
    'charge': -1,
    'pfRelIso03_all': -999.0,
    'dxy': -0.001959428656846285,
    'dxyErr': 0.002926760585978627,
    'dz': -0.0060557774268090725,
    'dzErr': 0.003230293281376362},
   {'pt': 6.690738201141357,
    'eta': 2.065934658050537,
    'phi': 1.6866998672485352,
    'mass': -0.005329584237188101,
    'charge': 1,
    'pfRelIso03_all': 0.5880627036094666,
    'dxy': 0.000966764404438436,
    'dxyErr': 0.014851272106170654,
    'dz': 2.7469565868377686,
    'dzErr': 0.027287257835268974}],
  'muon': [],
  'MET': {'pt': 19.061464309692383, 'phi': -2.1664631366729736}}]

For the rest of this lesson and your upcoming project, here’s the meaning of each field. (We only use a few of them.)

  • run (int): unique identifier for a data-taking period of the LHC. This is simulated data, so the run number is 1.

  • luminosityBlock (int): unique identifier for a period of relatively stable conditions within a run.

  • event (int): unique identifier for one crossing of LHC bunches.

  • PV (dict): primary vertex of the collision.

    • x (float): \(x\)-position in cm.

    • y (float): \(y\)-position in cm.

    • z (float): \(z\)-position (along the beamline) in cm.

  • electron (list of dict): list of electrons (may be empty).

    • pt (float): \(p_T\) component of momentum transverse to the beamline in GeV/\(c\).

    • eta (float): \(\eta\) pseudorapidity (roughly, polar angle with respect to the beamline), unitless.

    • phi (float): \(\phi\) azimuthal angle (in the plane that is perpendicular to the beamline), unitless.

    • mass (float): measured mass of the particle in GeV/\(c^2\).

    • charge (int): either +1 or -1, unitless.

    • pfRelIso03_all (float): quantity that specifies how isolated this electron is from the rest of the particles in the event, unitless.

    • dxy (float): distance of closest approach to the primary vertex in the plane that is perpendicular to the beamline, in cm.

    • dxyErr (float): uncertainty in the dxy measurement.

    • dz (float): distance of closest approach to the primary vertex in \(z\), along the beamline, in cm.

    • dzErr (float): uncertainty in the dz measurement.

  • muon (list of dict): list of muons (may be empty) with the same dict fields as electron.

  • MET (dict): missing transverse energy (in the plane perpendicular to the beamline).

    • pt (float): \(p_T\) magnitude, in GeV/\(c\).

    • phi (float): \(\phi\) aximuthal angle, unitless.

And here are some coordinate transformations:

  • \(p_x = p_T \cos\phi \cosh\eta\)

  • \(p_y = p_T \sin\phi \cosh\eta\)

  • \(p_z = p_T \sinh\eta\)

  • \(\displaystyle E = \sqrt{{p_x}^2 + {p_y}^2 + {p_z}^2 + m^2}\)

But, as usual, there’s a library for that: Vector.

import vector

def to_vector(particle):
    return vector.obj(
        pt=particle["pt"],
        eta=particle["eta"],
        phi=particle["phi"],
        mass=particle["mass"],
    )

for particle in dataset[0]["muon"]:
    v = to_vector(particle)
    print(v.E, v.px, v.py, v.pz)

80.03810173614954 -62.09642131826239 10.888704252275756 -49.31082178393471
53.837451985499946 19.5441283607252 -32.729005959017954 -38.01709205284513
4.260074277908423 2.05475040026448 3.4885342087314886 -1.3210598131215057

Plotting distributions of particles#

The most commonly used plotting package is Matplotlib.

The way that it is conventionally imported is a little odd.

import matplotlib.pyplot as plt

Although it’s possible to make plots directly from plt (when you’re in a hurry), you’ll usually want to structure notebook cells for plotting like this:

fig, ax = plt.subplots()

...

plt.show()
_images/8852035462ddaea257dd94f8f88f277b0993cb5e85d77d5a256d5d65b3ca98dc.png

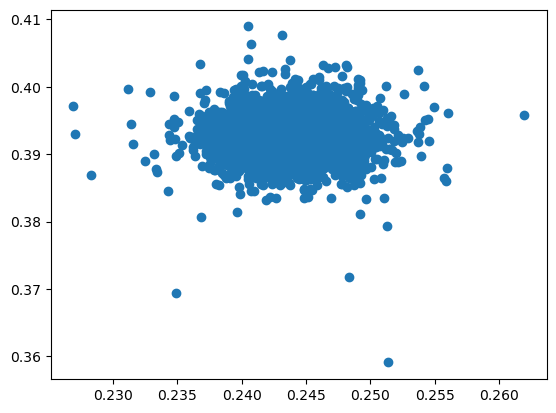
For example, this plots primary vertex y versus x.

Note the use of list comprehensions. Matplotlib wants \(x\) values and \(y\) values in separate collections, so we have to reformat them. This would be more complex without list comprehensions.

fig, ax = plt.subplots()

ax.scatter([event["PV"]["x"] for event in dataset], [event["PV"]["y"] for event in dataset])

plt.show()
_images/126a0cad9c5865ef4252920f576d017e705889b39e2d55d27dcfb4d89e5b7787.png

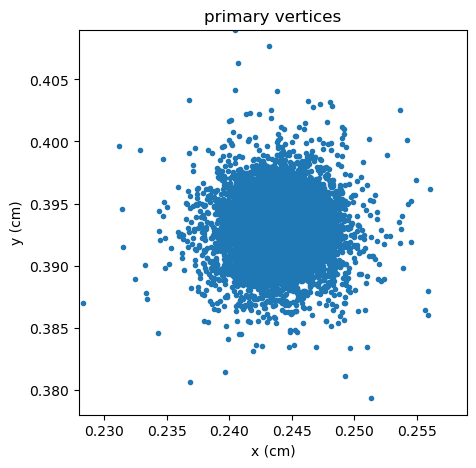
To make this plot more publication-ready, see the Matplotlib documentation or examples online.

fig, ax = plt.subplots(figsize=(5, 5))

ax.scatter(
    [event["PV"]["x"] for event in dataset],
    [event["PV"]["y"] for event in dataset],
    marker=".",
)

ax.set_xlim(0.228, 0.259)
ax.set_ylim(0.378, 0.409)
ax.set_xlabel("x (cm)")
ax.set_ylabel("y (cm)")
ax.set_title("primary vertices")

fig.savefig("/tmp/plot.pdf")
_images/7e1ae5d82de26c83224064b545de4775300e211d0b7ae6b09c66a910298f3a32.png

The plt.subplots gives you a place for whole-figure options (such as figsize) and it can be used to make several subplots.

fig, ((ax0, ax1, ax2), (ax3, ax4, ax5)) = plt.subplots(2, 3)

...

plt.show()
_images/979e715765325869079d7d44a5858f4b01c650280f05d9cb6e6ab70c62849b01.png

The ((ax0, ax1, ax2), (ax3, ax4, ax5)) syntax is “unpacking” two nested collections of axis objects—that’s something we can do whenever we know that a function returns a collection of a known size and we want them in separate variables. We can then use each axis object for separate plots.

The final plt.show() is unnecessary in Jupyter but necessary on a Python terminal. It also prevents Jupyter from printing the last Python object in the cell, which is usually just something you used to make the plot, not something you’re interested in.

Next, let’s make a plot of electron py versus px, using Vector for the coordinate transformation. The most complicated part is that electron collections are nested within the event collection. (This is possible in a list comprehension, but it would no longer be “simple”.)

fig, ax = plt.subplots()

px_values = []
py_values = []
for event in dataset:
    for electron in event["electron"]:
        v = to_vector(electron)
        px_values.append(v.px)
        py_values.append(v.py)

plt.scatter(px_values, py_values, marker=".")

plt.show()
_images/f87c6cde53e1e371b9fbbbf85774a51d3becb809b8b979c3c7f469125e694549.png

Plotting histograms#

Physicists usually want to plot histograms. Matplotlib’s built-in plt.hist function can be used when you’re in a hurry, but hist is a more feature-complete alternative for particle physicists.

from hist import Hist

For instance, you can create an empty histogram and fill it later.

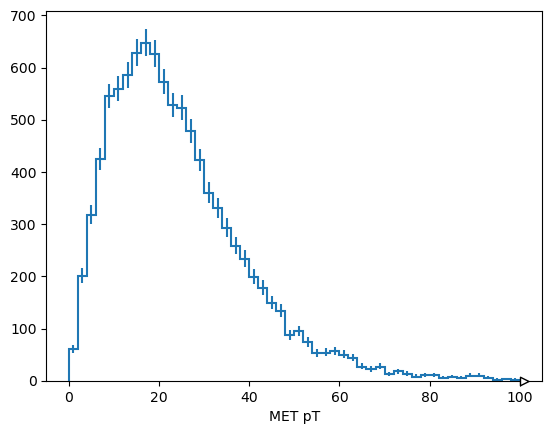
met_pt = Hist.new.Reg(50, 0, 100, name="MET pT").Double()
met_pt
0 100 MET pT
Regular(50, 0, 100, name='MET pT')
Double() Σ=0.0 
met_pt.fill([event["MET"]["pt"] for event in dataset])
met_pt
0 100 MET pT
Regular(50, 0, 100, name='MET pT')
Double() Σ=9967.0 (10000.0 with flow)

It can be used with Matplotlib by passing the axis object as an ax argument.

fig, ax = plt.subplots()

met_pt.plot1d(ax=ax)

plt.show()
_images/1cd6345c05e8d9feb2c3a9729c7180d9616f6f9fb596dbb4551ec916894589c2.png

Mini-quiz 6: Make a histogram of electron \(p_T\).

Lesson 1 project: finding Higgs decays#

As described in the intro, navigate to the notebooks directory and open lesson-1-project.ipynb, then follow its instructions. The projects are the most important parts of these lessons!