Lesson 4: Vertical and horizontal scaling#
This lesson is about making Python faster, in two dimensions: “vertical” scaling means accelerating a workload by improving its efficiency and “horizontal” scaling means accelerating a workload by running it on more processors.
We’ll start with vertical scaling.
Performance limitations of array-oriented code#
As a reminder, Python is slow for reasons that have to do with the interactive, dynamic environment that it provides. “Compile-first” languages that focus on speed are usually orders of magnitude faster than Python for equivalent code.
We’ve also seen that array-oriented computing can accelerate Python by offloading number-crunching to compiled code.
import numpy as np
import awkward as ak
events = ak.from_parquet("data/SMHiggsToZZTo4L.parquet")[:100000]
The following makes an array of lists of muon \(p_z = p_T \sinh(\eta)\) using (nested) list comprehensions and Awkward Array.
%%timeit -r1 -n1
pz = [[muon.pt * np.sinh(muon.eta) for muon in event.muon] for event in events]
15.8 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
%%timeit -r1 -n1
pz = events.muon.pt * np.sinh(events.muon.eta)
4.81 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
It’s thousands of times faster. And yet, the array-oriented solution is still giving up some computational efficiency because it makes multiple loops over the data.
In general, computing is much faster than memory access. While the fastest instructions (like addition) take about 1 CPU cycle to compute, accessing RAM takes about 240 cycles (What every programmer should know about memory, Ulrich Drepper (2007)). To prevent this difference in speed from starving the CPU, data streams from RAM into the CPU through a hierarchy of caches.
But if we stream a large array through the CPU to perform one mathematical operation, then do it again to perform another operation, the caches (which are smaller than the array) get overwritten before they can be used again.
Speed of compiled code#
Generally, a function written in a “compile-first” language provides a baseline: the fastest that the function can be executed. (“Generally” because it’s still possible to make performance mistakes.)
Let’s see that using C and the quadratic formula as examples. First, we have to create a file with the C function in it,
%%writefile quadratic_formula_c.c
#include <math.h>
void run(double* a, double* b, double* c, double* output) {
for (int i = 0; i < 1000000; i++) {
output[i] = (-b[i] + sqrt(b[i]*b[i] - 4*a[i]*c[i])) / (2*a[i]);
}
}
Writing quadratic_formula_c.c
then compile that file (with -O3 for all optimizations, -shared to make code that can be dynamically loaded instead of a full program, and -lm to make the math functions work),
! cc quadratic_formula_c.c -O3 -shared -lm -o quadratic_formula_c.so
and then load it into Python and tell Python how to use it.
import ctypes
pointer_double = ctypes.POINTER(ctypes.c_double)
quadratic_formula_c = ctypes.CDLL("./quadratic_formula_c.so")
quadratic_formula_c.run.argtypes = (pointer_double, pointer_double, pointer_double, pointer_double)
quadratic_formula_c.run.restype = None
def ptr(array):
return array.ctypes.data_as(pointer_double)
Now let’s test it on a million values.
a = np.random.uniform(5, 10, 1000000)
b = np.random.uniform(10, 20, 1000000)
c = np.random.uniform(-0.1, 0.1, 1000000)
%%timeit
output = np.empty(1000000)
quadratic_formula_c.run(ptr(a), ptr(b), ptr(c), ptr(output))
4.23 ms ± 9.12 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
%%timeit
output = (-b + np.sqrt(b**2 - 4*a*c)) / (2*a)
7.86 ms ± 27.5 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
The corresponding formula in NumPy is about 2× slower.
Hidden in the NumPy expression are intermediate arrays: each operation creates a new array, and most of them are only needed temporarily. The above is roughly equivalent to this:
%%timeit
tmp1 = np.negative(b) # -b
tmp2 = np.square(b) # b**2
tmp3 = np.multiply(4, a) # 4*a
tmp4 = np.multiply(tmp3, c) # tmp3*c
del tmp3
tmp5 = np.subtract(tmp2, tmp4) # tmp2 - tmp4
del tmp2, tmp4
tmp6 = np.sqrt(tmp5) # sqrt(tmp5)
del tmp5
tmp7 = np.add(tmp1, tmp6) # tmp1 + tmp6
del tmp1, tmp6
tmp8 = np.multiply(2, a) # 2*a
np.divide(tmp7, tmp8) # tmp7 / tmp8 This is the result!
8.78 ms ± 40.3 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
(“Roughly” because NumPy attempts to “fuse” some operations to avoid intermediate arrays, which accounts for this small difference in speed. But the 2× faster C function is completely “fused”.)
Remember, though, that NumPy is hundreds of times faster than a Python for loop,
%%timeit -r1 -n1
output = np.empty(1000000)
for i in range(len(output)):
output[i] = (-b[i] + np.sqrt(b[i]**2 - 4*a[i]*c[i])) / (2*a[i])
1.52 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
so the speed hierarchy has two steps:
with a much bigger gap between Python loops and NumPy than NumPy and compiled code. A generally good strategy is to figure out how you’re going to solve computational problems in Python and array-oriented code, which is more convenient because it is interactive, and then optimize the solution in compiled code when you think you’re done.
Getting compiled code into Python#
Methods of getting compiled code into Python have been developed throughout its history. The colors refer to different types of techniques.
We’ve already used Python’s built-in ctypes module, which lets us pass arrays to a compiled C function, but we have to know its types and any mistake could cause a segfault (the program would crash without giving us a prompt to figure out why) or undefined behavior (completely random errors).
pybind11#
The pybind11 package provides a safer way to do it, this time using C++ instead of C. The following file defines a Python module with a run function.
%%writefile quadratic_formula_pybind11.cpp
#include <pybind11/pybind11.h>
#include <pybind11/numpy.h>
namespace py = pybind11;
void run(
py::array_t<double, py::array::forcecast> a_numpy,
py::array_t<double, py::array::forcecast> b_numpy,
py::array_t<double, py::array::forcecast> c_numpy,
py::array_t<double> output_numpy
) {
const double* a = a_numpy.data();
const double* b = b_numpy.data();
const double* c = c_numpy.data();
double* output = output_numpy.mutable_data();
for (int i = 0; i < output_numpy.size(); i++) {
output[i] = (-b[i] + sqrt(b[i]*b[i] - 4*a[i]*c[i])) / (2*a[i]);
}
}
PYBIND11_MODULE(quadratic_formula_pybind11, m) {
m.def("run", &run);
}
Writing quadratic_formula_pybind11.cpp
The py::array_t type is templated to ensure that the NumPy array has double-valued numbers and applies a policy of forcing it to be cast if it does not. (The output_numpy can’t be cast or the function would fill a copy, rather than the array we give it.)
The compilation procedure is more complicated, but there are helper functions in Python.
import os
import sys
from pybind11 import get_include
inc = "-I " + get_include()
plat = "-undefined dynamic_lookup" if "darwin" in sys.platform else "-fPIC"
pyinc = !python3-config --cflags
! c++ -std=c++11 quadratic_formula_pybind11.cpp -O3 -shared {inc} {pyinc.s} -o quadratic_formula_pybind11.so {plat}
Now it’s a Python module that can be imported in the normal way.
import quadratic_formula_pybind11
output = np.zeros(1000000)
quadratic_formula_pybind11.run(a, b, c, output)
output
array([ 0.00216223, -0.00423167, -0.00693462, ..., 0.00251095,
-0.000587 , 0.00512748])
It’s about the same speed as the C function,
%%timeit
output = np.zeros(1000000)
quadratic_formula_pybind11.run(a, b, c, output)
4.67 ms ± 5.37 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
but much safer.
Important! As usual with array-oriented programming, the essential thing is that the loop over big datasets is in the compiled code. What do you think will happen in the following?
%%writefile quadratic_formula_pybind11_noloop.cpp
#include <pybind11/pybind11.h>
namespace py = pybind11;
double run(double a, double b, double c) {
return (-b + sqrt(b*b - 4*a*c)) / (2*a);
}
PYBIND11_MODULE(quadratic_formula_pybind11_noloop, m) {
m.def("run", &run);
}
Writing quadratic_formula_pybind11_noloop.cpp
! c++ -std=c++11 quadratic_formula_pybind11_noloop.cpp -O3 -shared {inc} {pyinc.s} -o quadratic_formula_pybind11_noloop.so {plat}
import quadratic_formula_pybind11_noloop
%%timeit -r1 -n1
output = np.zeros(1000000)
for i in range(len(output)):
output[i] = quadratic_formula_pybind11_noloop.run(a[i], b[i], c[i])
416 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
If you want to publish an accelerated Python module, pybind11 is a good choice. However, it has two problems if you’re using it interactively,
changing the C++ code, recompiling and reloading does not update the code that gets run (
importonly works once for compiled code),you have to use two languages: Python and C++.
Numba#
The Numba package lets you compile and recompile functions that are written in (a subset of) Python.
import numba as nb
@nb.jit
def quadratic_formula_numba(a_array, b_array, c_array):
output = np.empty(len(a_array))
for i, (a, b, c) in enumerate(zip(a_array, b_array, c_array)):
output[i] = (-b + np.sqrt(b**2 - 4*a*c)) / (2*a)
return output
Numba compiles the function the first time it is called, since it compiles a different version of the function for each combination of data types.
quadratic_formula_numba(a, b, c)
array([ 0.00216223, -0.00423167, -0.00693462, ..., 0.00251095,
-0.000587 , 0.00512748])
%%timeit
quadratic_formula_numba(a, b, c)
4.21 ms ± 7.19 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
The catch is that some code that works in Python,
def f():
x = "a string"
for i in range(5):
if i == 0:
x = 0
x = x + 1
return x
f()
5
does not work in Numba.
@nb.jit
def f():
x = "a string"
for i in range(5):
if i == 0:
x = 0
x = x + 1
return x
numba_error = None
try:
f()
except Exception as err:
numba_error = err
print(numba_error)
Failed in nopython mode pipeline (step: nopython frontend)
Cannot unify Literal[str](a string) and Literal[int](0) for 'x.3', defined at /tmp/ipykernel_4463/241084027.py (7)
File "../../../../../../tmp/ipykernel_4463/241084027.py", line 7:
<source missing, REPL/exec in use?>
During: typing of assignment at /tmp/ipykernel_4463/241084027.py (7)
File "../../../../../../tmp/ipykernel_4463/241084027.py", line 7:
<source missing, REPL/exec in use?>
In the case above, it’s because x = x + 1 would be wrong for x = "a string" and the compiler doesn’t recognize that x will always be an integer before it gets to that line. It can’t prove (mathematically) that the error never happens, so it can’t generate compiled code, which doesn’t check such things (which is what makes it fast).
Numba also can’t accept data types in compiled code that it does not recognize, because it wouldn’t know what compiled code to replace it with. For our purposes (the project for this lesson), Numba does recognize NumPy, Awkward Array, and Vector. See also
the Python features supported by Numba,
the NumPy functions supported by Numba.
Finally, note that Numba accelerates code written in imperative form, with for loops, since array-oriented code would create intermediate arrays, and then it doesn’t matter whether it’s in a compiled block or not.
@nb.jit
def quadratic_formula_numba_on_arrays(a, b, c):
tmp1 = np.negative(b) # -b
tmp2 = np.square(b) # b**2
tmp3 = np.multiply(4, a) # 4*a
tmp4 = np.multiply(tmp3, c) # tmp3*c
tmp5 = np.subtract(tmp2, tmp4) # tmp2 - tmp4
tmp6 = np.sqrt(tmp5) # sqrt(tmp5)
tmp7 = np.add(tmp1, tmp6) # tmp1 + tmp6
tmp8 = np.multiply(2, a) # 2*a
return np.divide(tmp7, tmp8) # tmp7 / tmp8
quadratic_formula_numba_on_arrays(a, b, c)
array([ 0.00216223, -0.00423167, -0.00693462, ..., 0.00251095,
-0.000587 , 0.00512748])
%%timeit
quadratic_formula_numba_on_arrays(a, b, c)
9.87 ms ± 28.6 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Julia#
Julia is a programming language that is based entirely on the idea of interactive (Just In Time, or JIT) compilation. It is like Numba, but for an entire language, without exceptions. It combines performance-oriented features like C++ with interactive convenience like Python in one language, but it is an entirely new language.
In particle physics (especially LHC), there’s a growing movement to use Julia, but it is not as widespread as Python (at the time of this writing). In particular,
UnROOT.jl is a Julia implementation of ROOT I/O, like Uproot for Python.
AwkwardArray.jl lets you pass data between Julia and Python as Awkward Arrays.
and there are many others.
Check it out if you’re interested!
JAX#
Whereas Numba and Julia (primarily) accelerate imperative code, JAX accelerates array-oriented code.
import jax
jax.config.update("jax_platform_name", "cpu")
@jax.jit
def quadratic_formula_jax(a, b, c):
return (-b + jax.numpy.sqrt(b**2 - 4*a*c)) / (2*a)
quadratic_formula_jax(a, b, c)
Array([ 0.00216227, -0.00423164, -0.0069346 , ..., 0.00251095,
-0.000587 , 0.00512751], dtype=float32)
%%timeit
quadratic_formula_jax(a, b, c)
1.44 ms ± 54.9 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
JAX recognizes code that would create intermediate arrays and “fuses” them so that they don’t.
@jax.jit
def quadratic_formula_jax_on_arrays(a, b, c):
tmp1 = jax.numpy.negative(b) # -b
tmp2 = jax.numpy.square(b) # b**2
tmp3 = jax.numpy.multiply(4, a) # 4*a
tmp4 = jax.numpy.multiply(tmp3, c) # tmp3*c
tmp5 = jax.numpy.subtract(tmp2, tmp4) # tmp2 - tmp4
tmp6 = jax.numpy.sqrt(tmp5) # sqrt(tmp5)
tmp7 = jax.numpy.add(tmp1, tmp6) # tmp1 + tmp6
tmp8 = jax.numpy.multiply(2, a) # 2*a
return jax.numpy.divide(tmp7, tmp8) # tmp7 / tmp8
quadratic_formula_jax_on_arrays(a, b, c)
Array([ 0.00216227, -0.00423164, -0.0069346 , ..., 0.00251095,
-0.000587 , 0.00512751], dtype=float32)
%%timeit
quadratic_formula_jax_on_arrays(a, b, c)
1.46 ms ± 44.9 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
So, in the end, choosing between imperative and array-oriented code is not strictly a question of performance.
Horizontal scaling#
Now that we’ve looked at several ways to vertically scale your code, let’s consider horizontal scaling.
If you have access to a batch queue, such as the LHC GRID, you can distribute a process by writing a Python script that takes a different subset of the data in each task. However,
you’d have to set that up by hand,
it only applies to “embarrassingly parallel” processes, in which the data in one computer is not needed by another.
These problems can be solved by a parallel processing framework that understands workload it is parallelizing. (This was the advancement that came with Hadoop in the Big Data movement of the early 2000’s.)
Dask#
In Python, Dask is a popular way to scale out array-oriented computations.
import dask
Dask replaces “eager” Python code, which computes values as soon as it is called, with “lazy” code, which returns a description of how to compute the values.
This is eager:
def increment(i):
return i + 1
def add(a, b):
return a + b
a, b = 1, 12
c = increment(a)
d = increment(b)
output = add(c, d)
output
15
This is lazy:
@dask.delayed
def increment(i):
return i + 1
@dask.delayed
def add(a, b):
return a + b
a, b = 1, 12
c = increment(a)
d = increment(b)
output = add(c, d)
output
Delayed('add-f70d77f7-553b-4b33-b6ac-628619607e13')
The lazy output is a set of instructions that can be executed with
output.compute()
15
or visualized with
output.visualize()
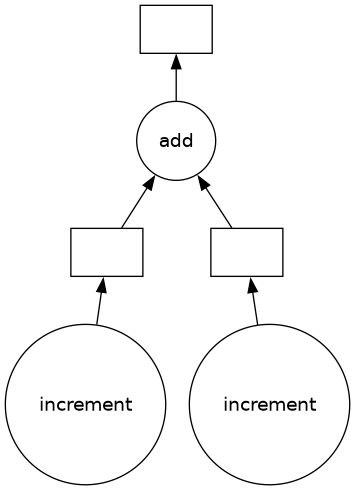
This set of instructions can now be sent to a computer cluster, which can ensure that each computer works on a different subset of the data.
Dask is especially intended for array-oriented programming. It has an array data type that can be operated on like a NumPy array. Here’s a lazy example of the quadratic formula.
import dask.array as da
a = da.random.uniform(5, 10, 1000000)
b = da.random.uniform(10, 20, 1000000)
c = da.random.uniform(-0.1, 0.1, 1000000)
output = (-b + np.sqrt(b**2 - 4*a*c)) / (2*a)
output
|
||||||||||||||||
This visualization of the output indicates the size, data type, and number of steps in the “instructions”, the Dask graph. Here’s what the graph looks like:
output.visualize()
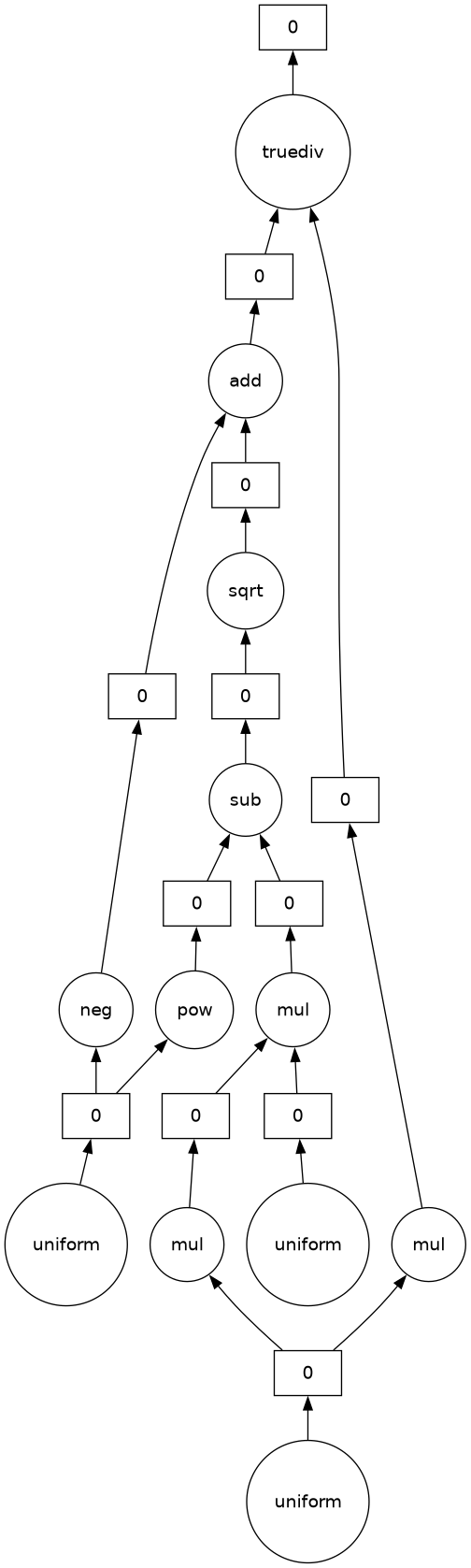
Every step in the formula is represented. If we want to see how a set of Dask workers would execute this, set optimize_graph=True.
output.visualize(optimize_graph=True)
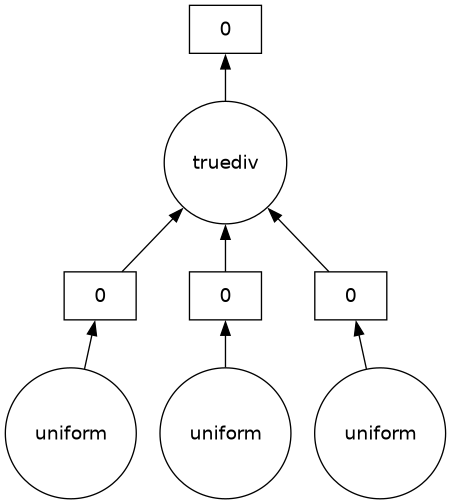
The three random arrays, a, b, c, can be generated separately, but they need to be on one worker to compute the quadratic formula (which ends with truediv).
Here is an example that you should try yourself, in the workbook, to see how the graph corresponds to a parallel process.
import time
@dask.delayed
def start():
print("start")
return 1
@dask.delayed
def concurrent(initial, i):
print(f"begin {i}")
time.sleep(np.random.uniform(0, 5))
print(f"end {i}")
return initial + i**2
@dask.delayed
def combine(partial_results):
print("combine")
return sum(partial_results)
initial = start()
output = combine([concurrent(initial, i) for i in range(10)])
The graph is shown below: a single task, start passes its output to 10 concurrent tasks, which all pass their output to combine.
output.visualize()
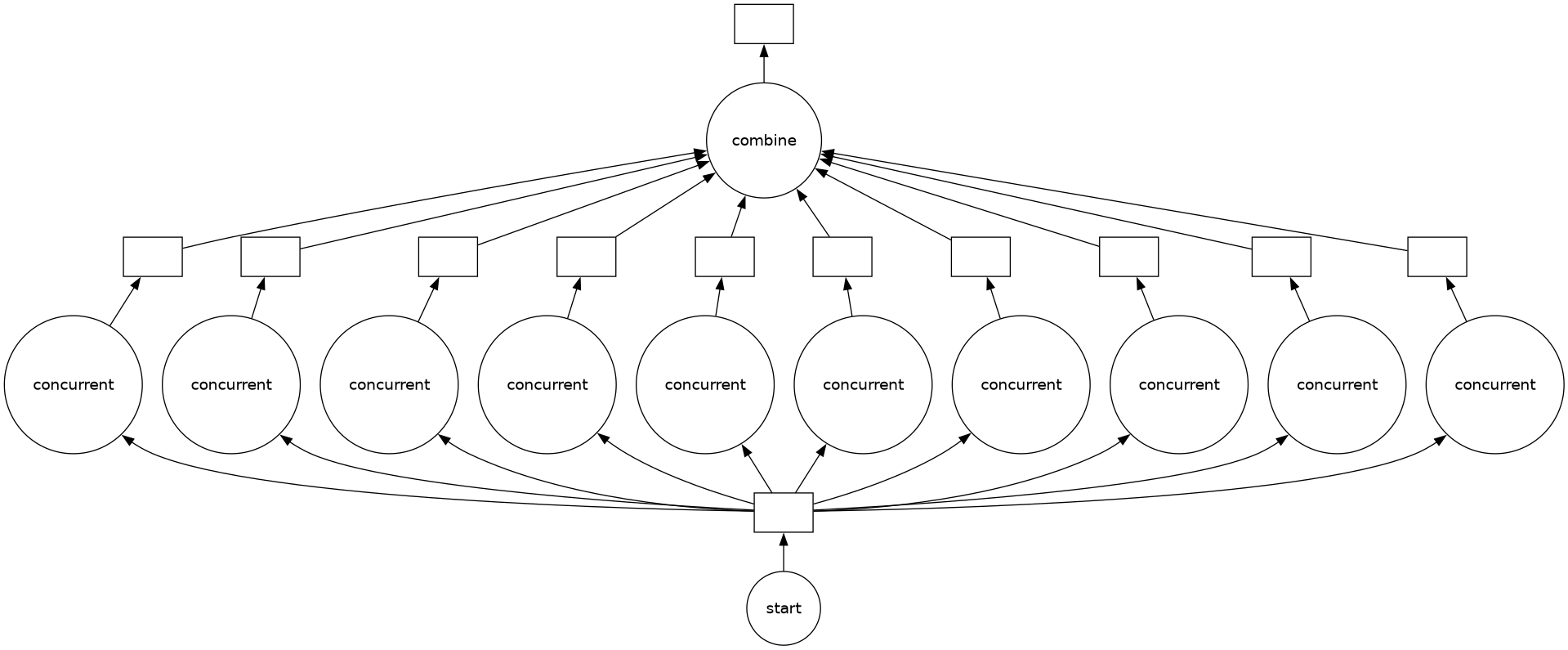
Here’s a sample run. The concurrent tasks begin in a random order and they finish after a random number of seconds (in a different order), and combine runs last. The whole process takes much less than the total time of all tasks (2.5 seconds × 10 tasks = 25 seconds) because concurrent are running in parallel.
output.compute()
begin 7
begin 1
begin 6
end 6
begin 3
end 1
begin 9
end 3
begin 8
end 7
begin 0
end 0
begin 2
end 9
end 8
end 2
combine
295
For debugging, you could run them synchronously to see the difference.
with dask.config.set(scheduler="synchronous"):
output.compute()
start
begin 5
end 5
begin 7
end 7
begin 1
end 1
begin 6
end 6
begin 3
end 3
begin 9
end 9
begin 8
end 8
begin 4
end 4
begin 0
end 0
begin 2
end 2
combine
Arrays can be processed in parallel if they have chunks smaller than the total size of the array. In the example below, the array has 1 million elements, but each chunk has 200 thousand elements, so there’s a total of 5 chunks.
a = da.random.uniform(5, 10, 1000000, chunks=200000)
b = da.random.uniform(10, 20, 1000000, chunks=200000)
c = da.random.uniform(-0.1, 0.1, 1000000, chunks=200000)
output_array = (-b + np.sqrt(b**2 - 4*a*c)) / (2*a)
output_array
|
||||||||||||||||
output_array.visualize(optimize_graph=True)
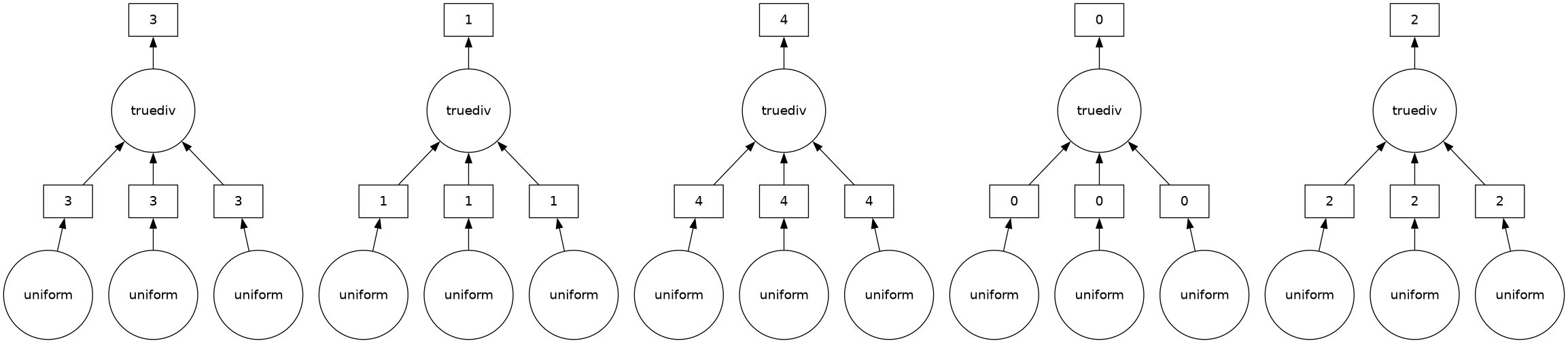
Thus, the following calculation can run in parallel on up to 5 processors, if the computer has at least 5 CPU cores (most do).
output_array.compute()
array([-0.00799416, 0.00027615, 0.00526769, ..., -0.00185101,
0.00228623, 0.00169946])
Dask clusters#
The above provides an easy way to parallelize across the CPUs on a single computer, but if a dataset is large enough, you’ll need a computer cluster.
If you don’t have access to an existing Dask cluster, but you have computers on a network you’re allowed to run large jobs on, you can set it up with one call to
dask scheduler # starts the scheduler
and as many of the following as you have CPU cores:
dask worker IP-ADDRESS-OF-SCHEDULER:8786
The Dask workers contact the scheduler through its network address (IP-ADDRESS-OF-SCHEDULER, which you need to know) on default port 8786.
I’ll start these now (using Python’s subprocess) with 3 workers, each with 1 thread for simplicity.
from subprocess import Popen, PIPE
scheduler = Popen(["dask-scheduler"], stdout=PIPE, stderr=PIPE, text=True)
time.sleep(0.5)
worker1 = Popen(["dask", "worker", "--nthreads", "1", "127.0.0.1:8786"], stdout=PIPE, stderr=PIPE, text=True)
worker2 = Popen(["dask", "worker", "--nthreads", "1", "127.0.0.1:8786"], stdout=PIPE, stderr=PIPE, text=True)
worker3 = Popen(["dask", "worker", "--nthreads", "1", "127.0.0.1:8786"], stdout=PIPE, stderr=PIPE, text=True)
time.sleep(0.5)
Once these are running, we can connect to it through the scheduler’s network address.
import dask.distributed
client = dask.distributed.Client("127.0.0.1:8786")
client
Client
Client-9ea9a8f1-dec1-11ef-916f-6045bd4b5a27
| Connection method: Direct | |
| Dashboard: http://127.0.0.1:8787/status |
Scheduler Info
Scheduler
Scheduler-b0e70040-a9e4-4d0c-a4ff-af22e7b384df
| Comm: tcp://10.1.0.163:8786 | Workers: 0 |
| Dashboard: http://10.1.0.163:8787/status | Total threads: 0 |
| Started: Just now | Total memory: 0 B |
Workers
When you run a Dask job now, it will go from the client to the scheduler, and from there to the workers.
output.compute()
295
Now that the job is done, let’s look at the server logs.
time.sleep(0.5)
worker1.terminate()
worker2.terminate()
worker3.terminate()
time.sleep(0.5)
scheduler.terminate()
The scheduler (hopefully!) says that it was contacted by 3 workers, received work from a client, and distributed it to the workers.
stdout, stderr = scheduler.communicate()
print(stderr)
/home/runner/micromamba/envs/array-oriented-programming/lib/python3.11/site-packages/distributed/cli/dask_scheduler.py:142: FutureWarning: dask-scheduler is deprecated and will be removed in a future release; use `dask scheduler` instead
warnings.warn(
2025-01-30 04:21:03,696 - distributed.scheduler - INFO - -----------------------------------------------
2025-01-30 04:21:04,027 - distributed.http.proxy - INFO - To route to workers diagnostics web server please install jupyter-server-proxy: python -m pip install jupyter-server-proxy
2025-01-30 04:21:04,066 - distributed.scheduler - INFO - State start
2025-01-30 04:21:04,069 - distributed.scheduler - INFO - -----------------------------------------------
2025-01-30 04:21:04,070 - distributed.scheduler - INFO - Scheduler at: tcp://10.1.0.163:8786
2025-01-30 04:21:04,071 - distributed.scheduler - INFO - dashboard at: http://10.1.0.163:8787/status
2025-01-30 04:21:04,071 - distributed.scheduler - INFO - Registering Worker plugin shuffle
2025-01-30 04:21:04,381 - distributed.scheduler - INFO - Receive client connection: Client-9ea9a8f1-dec1-11ef-916f-6045bd4b5a27
2025-01-30 04:21:04,607 - distributed.core - INFO - Starting established connection to tcp://127.0.0.1:39752
2025-01-30 04:21:05,524 - distributed.scheduler - INFO - Register worker addr: tcp://127.0.0.1:37283 name: tcp://127.0.0.1:37283
2025-01-30 04:21:05,524 - distributed.scheduler - INFO - Starting worker compute stream, tcp://127.0.0.1:37283
2025-01-30 04:21:05,524 - distributed.core - INFO - Starting established connection to tcp://127.0.0.1:39786
2025-01-30 04:21:05,820 - distributed.scheduler - INFO - Register worker addr: tcp://127.0.0.1:40531 name: tcp://127.0.0.1:40531
2025-01-30 04:21:05,820 - distributed.scheduler - INFO - Starting worker compute stream, tcp://127.0.0.1:40531
2025-01-30 04:21:05,820 - distributed.core - INFO - Starting established connection to tcp://127.0.0.1:39790
2025-01-30 04:21:05,822 - distributed.scheduler - INFO - Register worker addr: tcp://127.0.0.1:44857 name: tcp://127.0.0.1:44857
2025-01-30 04:21:05,823 - distributed.scheduler - INFO - Starting worker compute stream, tcp://127.0.0.1:44857
2025-01-30 04:21:05,823 - distributed.core - INFO - Starting established connection to tcp://127.0.0.1:39788
2025-01-30 04:21:15,511 - distributed.core - INFO - Received 'close-stream' from tcp://127.0.0.1:39790; closing.
2025-01-30 04:21:15,512 - distributed.scheduler - INFO - Remove worker addr: tcp://127.0.0.1:40531 name: tcp://127.0.0.1:40531 (stimulus_id='handle-worker-cleanup-1738210875.5119808')
2025-01-30 04:21:15,512 - distributed.core - INFO - Received 'close-stream' from tcp://127.0.0.1:39788; closing.
2025-01-30 04:21:15,512 - distributed.scheduler - INFO - Remove worker addr: tcp://127.0.0.1:44857 name: tcp://127.0.0.1:44857 (stimulus_id='handle-worker-cleanup-1738210875.5127847')
2025-01-30 04:21:15,513 - distributed.core - INFO - Received 'close-stream' from tcp://127.0.0.1:39786; closing.
2025-01-30 04:21:15,513 - distributed.scheduler - INFO - Remove worker addr: tcp://127.0.0.1:37283 name: tcp://127.0.0.1:37283 (stimulus_id='handle-worker-cleanup-1738210875.51326')
2025-01-30 04:21:15,513 - distributed.scheduler - INFO - Lost all workers
2025-01-30 04:21:16,009 - distributed._signals - INFO - Received signal SIGTERM (15)
2025-01-30 04:21:16,009 - distributed.scheduler - INFO - Closing scheduler. Reason: signal-15
2025-01-30 04:21:16,010 - distributed.scheduler - INFO - Scheduler closing all comms
2025-01-30 04:21:16,011 - distributed.scheduler - INFO - Stopped scheduler at 'tcp://10.1.0.163:8786'
2025-01-30 04:21:16,011 - distributed.scheduler - INFO - End scheduler
The worker logs are similar: they received work and did it.
stdout1, stderr1 = worker1.communicate()
stdout2, stderr2 = worker2.communicate()
stdout3, stderr3 = worker3.communicate()
print(stderr1)
2025-01-30 04:21:04,610 - distributed.nanny - INFO - Start Nanny at: 'tcp://127.0.0.1:34949'
2025-01-30 04:21:05,603 - distributed.worker - INFO - Start worker at: tcp://127.0.0.1:44857
2025-01-30 04:21:05,603 - distributed.worker - INFO - Listening to: tcp://127.0.0.1:44857
2025-01-30 04:21:05,603 - distributed.worker - INFO - dashboard at: 127.0.0.1:40357
2025-01-30 04:21:05,603 - distributed.worker - INFO - Waiting to connect to: tcp://127.0.0.1:8786
2025-01-30 04:21:05,603 - distributed.worker - INFO - -------------------------------------------------
2025-01-30 04:21:05,603 - distributed.worker - INFO - Threads: 1
2025-01-30 04:21:05,603 - distributed.worker - INFO - Memory: 3.90 GiB
2025-01-30 04:21:05,603 - distributed.worker - INFO - Local Directory: /tmp/dask-scratch-space/worker-elvn_9i6
2025-01-30 04:21:05,603 - distributed.worker - INFO - -------------------------------------------------
2025-01-30 04:21:05,823 - distributed.worker - INFO - Starting Worker plugin shuffle
2025-01-30 04:21:05,824 - distributed.worker - INFO - Registered to: tcp://127.0.0.1:8786
2025-01-30 04:21:05,824 - distributed.worker - INFO - -------------------------------------------------
2025-01-30 04:21:05,824 - distributed.core - INFO - Starting established connection to tcp://127.0.0.1:8786
2025-01-30 04:21:15,509 - distributed._signals - INFO - Received signal SIGTERM (15)
2025-01-30 04:21:15,509 - distributed.nanny - INFO - Closing Nanny at 'tcp://127.0.0.1:34949'. Reason: signal-15
2025-01-30 04:21:15,509 - distributed.nanny - INFO - Nanny asking worker to close. Reason: signal-15
2025-01-30 04:21:15,510 - distributed.worker - INFO - Stopping worker at tcp://127.0.0.1:44857. Reason: signal-15
2025-01-30 04:21:15,510 - distributed.worker - INFO - Removing Worker plugin shuffle
2025-01-30 04:21:15,511 - distributed.core - INFO - Connection to tcp://127.0.0.1:8786 has been closed.
2025-01-30 04:21:15,512 - distributed.nanny - INFO - Worker closed
2025-01-30 04:21:15,748 - distributed.nanny - INFO - Nanny at 'tcp://127.0.0.1:34949' closed.
2025-01-30 04:21:15,748 - distributed.dask_worker - INFO - End worker
More interesting, though, is that each took on a different set of concurrent tasks.
print(stdout1)
begin 9
end 9
begin 3
end 3
print(stdout2)
begin 6
end 6
begin 1
end 1
begin 0
end 0
print(stdout3)
start
begin 5
end 5
begin 7
end 7
begin 8
end 8
begin 2
end 2
begin 4
end 4
combine
Dask collections#
Although you can build general computations with @dask.delayed, you would have to describe how to parallelize the work as a graph, as we did with the concurrent tasks above.
Dask collection types, like array, know how to parallelize over a chunked dataset (also called “partitions”).
import h5py
from hist import Hist
This calculation of Z boson mass is distributed over (at most) 4 CPU cores.
dataset_hdf5 = h5py.File("data/SMHiggsToZZTo4L.h5")
pt1 = da.from_array(dataset_hdf5["ee_mumu"]["e1"]["pt"], chunks=10000)
phi1 = da.from_array(dataset_hdf5["ee_mumu"]["e1"]["phi"], chunks=10000)
eta1 = da.from_array(dataset_hdf5["ee_mumu"]["e1"]["eta"], chunks=10000)
pt2 = da.from_array(dataset_hdf5["ee_mumu"]["e2"]["pt"], chunks=10000)
phi2 = da.from_array(dataset_hdf5["ee_mumu"]["e2"]["phi"], chunks=10000)
eta2 = da.from_array(dataset_hdf5["ee_mumu"]["e2"]["eta"], chunks=10000)
mass = np.sqrt(2*pt1*pt2*(np.cosh(eta1 - eta2) - np.cos(phi1 - phi2)))
mass
|
||||||||||||||||
with dask.config.set(scheduler="threads"):
Hist.new.Reg(120, 0, 120, name="dimuon mass").Double().fill(
mass.compute()
).plot();
/home/runner/micromamba/envs/array-oriented-programming/lib/python3.11/site-packages/dask/base.py:1103: UserWarning: Running on a single-machine scheduler when a distributed client is active might lead to unexpected results.
warnings.warn(
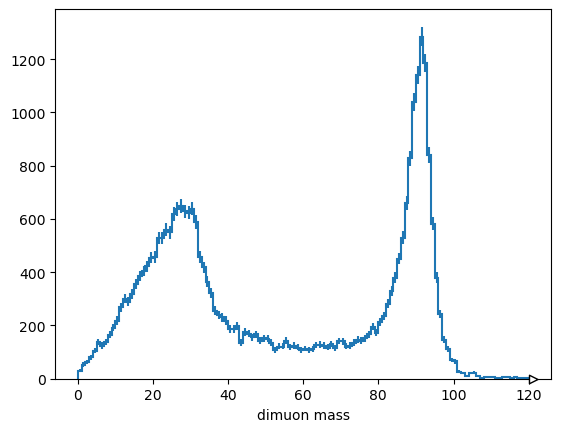
The general flow is that Dask collections are used to make graphs, which get submitted to clusters to run.
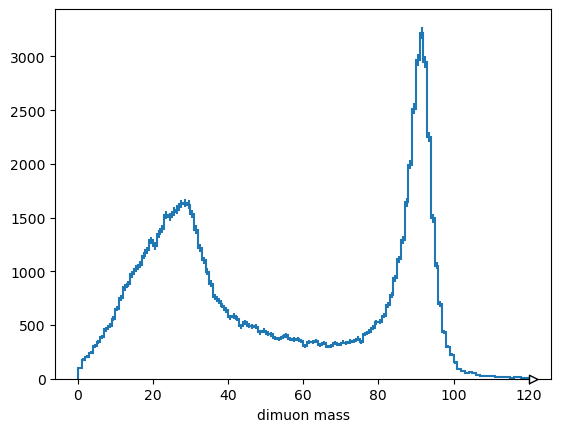
In addition to the collection types listed above, there is a dask-awkward package for lazy Awkward Arrays. uproot.dask opens ROOT files lazily, either producing Dask arrays (library="np") or dask-awkward arrays (library="ak").
import uproot
import awkward as ak
import dask_awkward as dak
events = uproot.dask("data/SMHiggsToZZTo4L.root")
events
dask.awkward<from-uproot, npartitions=1>
selected = events[ak.num(events.Electron_pt) == 2]
pt1 = selected.Electron_pt[:, 0]
phi1 = selected.Electron_phi[:, 0]
eta1 = selected.Electron_eta[:, 0]
pt2 = selected.Electron_pt[:, 1]
phi2 = selected.Electron_phi[:, 1]
eta2 = selected.Electron_eta[:, 1]
mass = np.sqrt(2*pt1*pt2*(np.cosh(eta1 - eta2) - np.cos(phi1 - phi2)))
mass
dask.awkward<sqrt, npartitions=1>
with dask.config.set(scheduler="threads"):
Hist.new.Reg(120, 0, 120, name="dimuon mass").Double().fill(
mass.compute()
).plot();
/home/runner/micromamba/envs/array-oriented-programming/lib/python3.11/site-packages/dask/base.py:1103: UserWarning: Running on a single-machine scheduler when a distributed client is active might lead to unexpected results.
warnings.warn(
Lesson 4 project: JIT-compiled Higgs combinatorics#
As described in the intro, navigate to the notebooks directory and open lesson-4-project.ipynb, then follow its instructions.