Lesson 2: Array-oriented programming#
Programming paradigms, such as “imperative”, “object-oriented”, and “functional”, are general styles of programming. Some programming languages favor one over the others, or make it easier to use one, rather than the others. For instance, C++ enables object-oriented programming in C.
In array-oriented programming, the primary data type is an array and most functions perform one operation on all values of the array.
Simple example of imperative, functional, and array-oriented#
Below are three solutions to the following problem: compute the square of each value in a collection of numbers.
Imperative#
Imperative programming is likely to be the most familiar: you supply a sequence of commands and the computer follows them one by one.
original = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
result = []
for x in original:
result.append(x**2)
result
[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
Functional#
Functional programming takes seriously the idea that functions are objects that can be passed around like any other data. Functional programming environments have a suite of predefined functions-that-take-functions such as map (apply a given function to every member of a collection, returning a collection), filter (use a boolean function to determine which values to keep), and reduce (apply a function to pairs of values in the collection to return a scalar).
In the following, Python’s lambda keyword defines a function as an expression without assigning it to a variable name (as def does).
original = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
result = list(map(lambda x: x**2, original))
result
[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
Python is not very friendly toward functional programming, since many of its functions (like list.append) change data in ways other than through the return value, and because the syntax for creating a lambda function is so long. (Compare lambda x: x**2 in Python with \x -> x**2 in Haskell.)
In Python, we often use list comprehensions where we would otherwise use map and filter.
original = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
result = [x**2 for x in original]
result
[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
Array-oriented#
Array-oriented programming is a little different from functional programming: instead of writing (lambda) functions and passing them to explicit calls of map, filter, and reduce, you use precompiled functions implicitly when you write expressions involving arrays.
import numpy as np
original = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
result = original**2
result
array([ 1, 4, 9, 16, 25, 36, 49, 64, 81, 100])
This formalism has the property that any mathematical expression on scalar numbers can also be applied to equal-length arrays of numbers. For example,
def quadratic_formula(a, b, c):
return (-b + np.sqrt(b**2 - 4*a*c)) / (2*a)
computes the (positive) quadratic formula
once if a, b, and c are scalar numbers,
a = 5
b = 10
c = -0.1
quadratic_formula(a, b, c)
np.float64(0.009950493836207741)
or a million times if they are arrays of length 1 million.
a = np.random.uniform(5, 10, 1000000)
b = np.random.uniform(10, 20, 1000000)
c = np.random.uniform(-0.1, 0.1, 1000000)
quadratic_formula(a, b, c)
array([-0.00543118, 0.00259879, 0.00462289, ..., 0.0087851 ,
-0.00444219, 0.00579801])
Complex example of imperative, functional, and array-oriented#
With a simple example, it’s easy to see exactly what it’s doing, but it doesn’t convey the “flavor” of how these paradigms differ in practice.
Here is a complex example. You don’t have to understand the details of how each solution works—just see how they follow different approaches and how the code generally looks. The problem is to compute gravitational forces among \(n\) particles in 3 dimensions.
Imperative#
def imperative_forces(m, x, p):
total_force = np.zeros_like(x)
for i in range(len(x)):
for j in range(i + 1, len(x)):
mi, mj = m[i], m[j]
xi, xj = x[i], x[j]
pi, pj = p[i], p[j]
displacement = [
xj[0] - xi[0],
xj[1] - xi[1],
xj[2] - xi[2],
]
distance = np.sqrt(displacement[0]**2 + displacement[1]**2 + displacement[2]**2)
direction = [
displacement[0] / distance,
displacement[1] / distance,
displacement[2] / distance,
]
force = [
G * mi * mj * direction[0] / distance**2,
G * mi * mj * direction[1] / distance**2,
G * mi * mj * direction[2] / distance**2,
]
total_force[i, 0] += force[0]
total_force[i, 1] += force[1]
total_force[i, 2] += force[2]
total_force[j, 0] += -force[0]
total_force[j, 1] += -force[1]
total_force[j, 2] += -force[2]
return total_force
The imperative solution is a long sequence of commands in nested for loops.
Functional#
from functools import reduce
from itertools import combinations
def functional_forces(m, x, p):
def negate(vector):
return [-a for a in vector]
def add(*vectors):
return [reduce(lambda a, b: a + b, components) for components in zip(*vectors)]
def subtract(vectorA, vectorB):
return add(vectorA, negate(vectorB))
def magnitude(vector):
return np.sqrt(reduce(lambda a, b: a + b, map(lambda a: a**2, vector)))
def force(mi, mj, xi, xj, pi, pj):
displacement = subtract(xi, xj)
distance = magnitude(displacement)
direction = [a / distance for a in displacement]
return [G * mi * mj * a / distance**2 for a in direction]
pairwise_forces = [
((i, j), force(mi, mj, xi, xj, pi, pj))
for ((i, (mi, xi, pi)), (j, (mj, xj, pj))) in combinations(enumerate(zip(m, x, p)), 2)
]
def partial_forces(pairwise_forces, i):
return (
[force for (_, check), force in pairwise_forces if i == check] +
[negate(force) for (check, _), force in pairwise_forces if i == check]
)
return np.array([add(*partial_forces(pairwise_forces, i)) for i in range(len(m))])
The functional solution defines many small functions and applies them in two list comprehensions.
Array-oriented#
def array_forces(m, x, p):
i, j = np.triu_indices(len(x), k=1)
pw_displacement = x[j] - x[i]
pw_distance = np.sqrt(np.sum(pw_displacement**2, axis=-1))
pw_direction = pw_displacement / pw_distance[:, np.newaxis]
pw_force = G * m[i, np.newaxis] * m[j, np.newaxis] * pw_direction / pw_distance[:, np.newaxis]**2
total_force = np.zeros_like(x)
np.add.at(total_force, i, pw_force)
np.add.at(total_force, j, -pw_force)
return total_force
The array-oriented solution is very concise—maybe even “dense”—and it invovles special NumPy functions such as np.triu_indices for the \(n (n - 1) / 2\) combinatorics and advanced slicing in square brackets ([ ]).
Comparison of the three solutions#
First, let’s just verify that they give the same result in a numerical example.
# three masses
m = np.array([2, 10, 1.1])
# initial position (x) and momentum (p) for each of the three
x = np.array([[0.1, 0.1, 0], [2, 0.9, 0.1], [-5, 1.5, -0.1]])
p = np.array([[3, -1, 0.5], [-13, 0, -0.2], [-10, 0.1, 0]])
G = 1
imperative_test = imperative_forces(m, x, p)
imperative_test
array([[ 4.24603602, 1.84053459, 0.22597908],
[-4.54361383, -1.80071551, -0.23380178],
[ 0.29757782, -0.03981909, 0.0078227 ]])
functional_test = functional_forces(m, x, p)
functional_test
array([[ 4.24603602, 1.84053459, 0.22597908],
[-4.54361383, -1.80071551, -0.23380178],
[ 0.29757782, -0.03981909, 0.0078227 ]])
array_test = array_forces(m, x, p)
array_test
array([[ 4.24603602, 1.84053459, 0.22597908],
[-4.54361383, -1.80071551, -0.23380178],
[ 0.29757782, -0.03981909, 0.0078227 ]])
np.allclose(imperative_test, functional_test)
True
np.allclose(functional_test, array_test)
True
(It could be more carefully tested at more points.)
Now compare the time to compute a sample of 500 planets.
m = np.ones(500)
x = np.random.normal(0, 1, (500, 3))
p = np.random.normal(0, 1, (500, 3))
%%timeit -n1 -r1
imperative_forces(m, x, p)
581 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
%%timeit -n1 -r1
functional_forces(m, x, p)
4.39 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
%%timeit -n1 -r1
array_forces(m, x, p)
25.2 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
Note the units: array-oriented is 30× faster than imperative and 300× faster than functional.
There are good reasons for this, which we’ll examine in the next section.
For now, though, which one would you choose if you wanted to calculate forces repeatedly, to make animations of planetary orbits?
import matplotlib.pyplot as plt
from matplotlib import animation
from IPython.display import HTML
def array_step(m, x, p, dt):
# this is a numerically stable way of updating positions, momenta, and forces
p += array_forces(m, x, p) * (dt/2) # half kick
x += p * dt / m[:, np.newaxis] # full drift
p += array_forces(m, x, p) * (dt/2) # half kick
def plot(m, x, p, dt, num_frames=100, steps_per_frame=10):
num_particles = len(m)
history = np.empty((num_frames, num_particles, 2))
for i in range(num_frames):
history[i, :, 0] = x[:, 0]
history[i, :, 1] = x[:, 1]
for _ in range(steps_per_frame):
array_step(m, x, p, dt)
fig, ax = plt.subplots(figsize=(5, 5))
lines = []
for j in range(num_particles):
lines.append(ax.plot(history[:1, j, 0], history[:1, j, 1])[0])
dots = ax.scatter(history[0, :, 0], history[0, :, 1])
ax.set_xlim(-2, 2)
ax.set_ylim(-2, 2)
def update(i):
for j, line in enumerate(lines):
line.set_xdata(history[:i, j, 0])
line.set_ydata(history[:i, j, 1])
dots.set_offsets(history[i, :, :])
return [*lines, dots]
ani = animation.FuncAnimation(fig=fig, func=update, frames=num_frames, interval=50, blit=True)
out = HTML(ani.to_jshtml())
plt.close()
return out
Double-planet orbits a star:
m = np.array([100, 1, 1], np.float64)
x = np.array([[0, 0, 0], [0, 0.9, 0], [0, 1.1, 0]], np.float64)
p = np.array([[0, 0, 0], [-13, 0, 0], [-10, 0, 0]], np.float64)
plot(m, x, p, dt=0.001)
Solution to the three-body problem!
a = 0.347111
b = 0.532728
m = np.array([1, 1, 1], np.float64)
x = np.array([[-1, 0, 0], [1, 0, 0], [0, 0, 0]], np.float64)
p = np.array([[a, b, 0], [a, b, 0], [-2 * a, -2 * b, 0]], np.float64)
plot(m, x, p, dt=0.01)
Chaos!
m = np.ones(25)
x = np.random.normal(0, 1, (25, 3))
p = np.random.normal(0, 1, (25, 3))
plot(m, x, p, dt=0.0025)
Why is array-oriented programming fast?#
A better question is, “Why is Python code slow?”
Roughly speaking, there are two types of languages—the “compile-first” ones, which are fast, and interactive ones, which are slow. This plot shows execution times for 10 scientific problems implemented in 12 languages (Debian Benchmarks Game).
Python, Ruby, Perl, Lua, and PHP all have the following in common:
they run instructions on an emulated virtual machine, rather than the physical computer,
they are dynamically typed, checking the types of each function call immediately before execution, rather than once in a compilation phase,
they all do many other dynamic, high-level things, like using garbage collectors, representing all values as objects, managing their own heap of memory, etc.
Thus, there’s a speed penalty for every line of Python code that is much larger than an equivalent line of compiled code.
However, a single NumPy function call that performs a million numerical calculations avoids Python’s speed trap without giving up on interactivity. In the gravitational force calculation on 500 planets (above),
imperative_forcesmakes Python loop over 500 × 499 pairs of planets, and on each pair it steps through 25 lines of Python code (214 virtual machine instructions),functional_forceshas a Python list comprehension over 500 × 499 pairs of planets, each of which calls 6 functions with a total of 12 lines of Python code (100 virtual machine instructions), plus all of the function call-stack overhead,array_forcessteps through 9 lines of Python code (103 virtual machine instructions) once. The loop over 500 × 499 pairs of planets is in compiled code, not Python code.
Here is a similar argument for the simple problem of squaring numbers:
original = np.random.poisson(3.14, 1000000)
def imperative_squares(original):
result = []
for x in original:
result.append(x**2)
return result
%%timeit
imperative_squares(original)
93.6 ms ± 1.55 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
import dis # dissasembler; shows us the Python virtual machine instructions
dis.dis(imperative_squares)
1 0 RESUME 0
2 2 BUILD_LIST 0
4 STORE_FAST 1 (result)
3 6 LOAD_FAST 0 (original)
8 GET_ITER
>> 10 FOR_ITER 26 (to 64)
12 STORE_FAST 2 (x)
4 14 LOAD_FAST 1 (result)
16 LOAD_METHOD 0 (append)
38 LOAD_FAST 2 (x)
40 LOAD_CONST 1 (2)
42 BINARY_OP 8 (**)
46 PRECALL 1
50 CALL 1
60 POP_TOP
62 JUMP_BACKWARD 27 (to 10)
5 >> 64 LOAD_FAST 1 (result)
66 RETURN_VALUE
It steps from FOR_ITER to JUMP_BACKWARD a million times and has to verify that x is an integer every time it gets to BINARY_OP.
On the other hand, in the array-oriented solution:
def array_squares(original):
return original**2
%%timeit
array_squares(original)
204 μs ± 1.92 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
dis.dis(array_squares)
1 0 RESUME 0
2 2 LOAD_FAST 0 (original)
4 LOAD_CONST 1 (2)
6 BINARY_OP 8 (**)
10 RETURN_VALUE
It steps through the above once and runs NumPy’s compiled code when it gets to BINARY_OP. It checks array types once so that it can assume that the numeric types are correct in the loop over a million integers. The physical CPU applies even more optimizations (memory prefetching, instruction pipelining, and maybe vector instructions).
Why does it use less memory?#
Arrays also use less memory than Python lists.
from pympler.tracker import SummaryTracker
memory_tracker = SummaryTracker()
memory_tracker.diff()
list_of_numbers = list(range(1000000))
array_of_numbers = np.arange(1000000)
memory_tracker.print_diff()
del list_of_numbers, array_of_numbers
types | # objects | total size
=============== | =========== | ============
int | 999742 | 26.70 MB
list | 2 | 7.63 MB
numpy.ndarray | 1 | 7.63 MB
str | 1 | 70 B
The base list and NumPy array are both 7.63 MB, but Python also requires 26.70 MB for 999743 integers.
Naively, 1000000 × 8-byte integers should be
1000000 * 8 / 1024**2
7.62939453125
MB. So what does Python need the extra 26.70 MB for?
Here’s the memory layout of a Python list of numbers:
and here’s the memory layout of a NumPy array of numbers:
So if you’re dealing with large datasets in Python, putting them in arrays is a good idea!
Expressiveness of array-oriented programming#
The performance advantages of array-oriented programming would not be useful if it were hard to express what you need to calculate. Unlike functional programming, you cannot write a function to map it over a dataset: you have to piece together the calculation you want to perform using the precompiled functions NumPy provides.
As an indication of what array-oriented programming is good for, here’s a timeline of all the array-oriented programming languages and libraries (that I know about):
All of them are interactive, data analysis environments. They all feature
an interactive REPL (read-evaluate-print loop),
concise notation,
a mathematical outlook.
This paradigm started mathematical and concise (perhaps too much): in the original language, APL,
np.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
was
(⍳10) - 1
np.sum(np.arange(1, 11))
np.int64(55)
was
+/⍳10
and
np.cumsum(np.arange(1, 11))
array([ 1, 3, 6, 10, 15, 21, 28, 36, 45, 55])
was
+\⍳10
It had a special keyboard for mathematical symbols and writing a one-line program was hard enough to celebrate by printing it on a T-shirt.
Modern array-oriented environments like NumPy are a step back, away from extreme conciseness.
Example of an array-oriented conversation#
A programming paradigm brings some concepts into the foreground and pushes others into the background:
paradigm |
emphasizes |
|---|---|
imperative/procedural |
low-level algorithms |
object-oriented |
large-scale program structure |
actor-based |
temporal locality |
literate |
human instruction |
event-driven |
cause-and-effect |
declarative |
properties of desired result |
symbolic |
formula transformations |
functional |
data transformations |
array-oriented |
data distributions |
Array-oriented programming emphasizes data distributions. Each precompiled step, which you can’t step through to examine or debug, iterates over all values in an array. Each interactive step lets you decide what will be the next operation you want to perform. It’s one mathematical operation at a time, rather than one data point at a time.
Suppose that you have a large dataset.
dataset = np.random.normal(0, 1, 1000000) # one MILLION data points
You’re not very interested in the first, or second, or third value in the dataset. You’re interested in their distribution, so you plot it.
plt.hist(dataset, bins=100, range=(-5, 5));
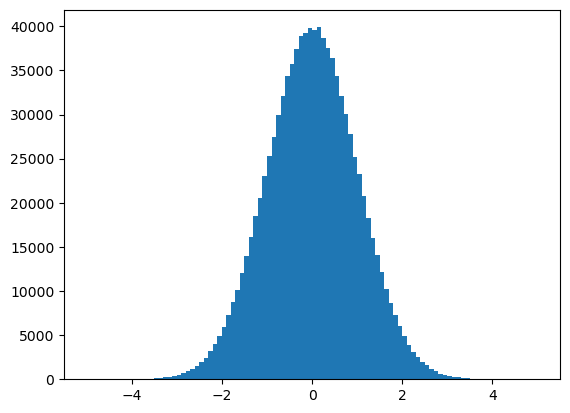
It’s a Gaussian (normal) distribution.
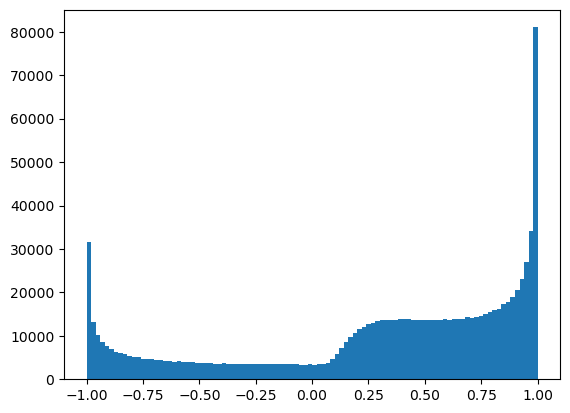
What happens if we square all values in the dataset?
dataset2 = dataset**2
plt.hist(dataset2, bins=100, range=(-5, 5));
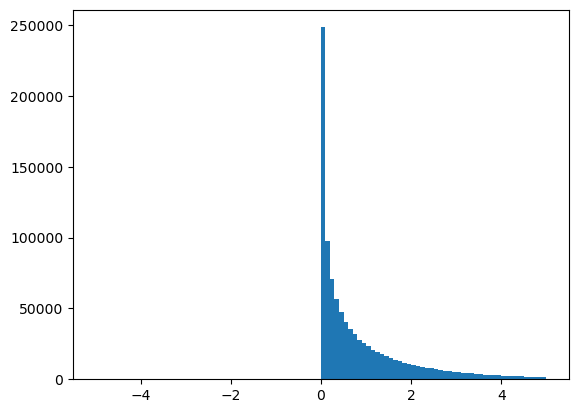
Okay, what if we compute this function?
dataset3 = np.sin(1/dataset2)
What happens to the distribution? Can you guess? (I can’t.)
plt.hist(dataset3, bins=100, range=(-1, 1));
In a data analysis, you’ll be investigating some effect, such as a source of systematics. You’ll apply a cut and look at the result—maybe that makes things better. You’ll try to apply a transformation to narrow in on the effect—maybe that makes things worse, so you back up to what you had previously. Then you apply it step by step and discover your error on one of the steps. Then you put the whole expression together again and move on.
This combination of interactivity between operations and high-performance in operations over a whole dataset is a perfect fit for investigative data analysis.
NumPy features#
The main features you’ll likely use from NumPy are:
reading and creating arrays,
elementwise arithmetic operations (
+-*/, etc.) and comparisons (==!=<<=>>=),universal functions (ufunc), which are precompiled elementwise functions like
sqrt,sin,cos,slicing in ranges (like Python lists), in multiple dimensions, and advanced slicing with arrays of booleans and integers,
reductions, such as sum, min/max, mean over an axis or over everything,
For most of these, the documentation is the best source. Here, let’s focus on slicing and reductions.
Slicing#
Python’s slicing syntax, which works on containers like list and tuple, is
container[start:stop:step]
If
startorstopis non-negative, it counts from the beginning of the container with0as the first item.If
startorstopis negative, it counts from the end of the container with-1as the first item.The
stepindicates how many items between each step:1is normal,2skips every other item,-1goes backward, and0is not allowed.Any of the three can be left out to get a reasonable default.
container = [0.0, 1.1, 2.2, 3.3, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9]
container[2:]
[2.2, 3.3, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9]
container[:5]
[0.0, 1.1, 2.2, 3.3, 4.4]
container[-6:-2]
[4.4, 5.5, 6.6, 7.7]
container[4:10:2]
[4.4, 6.6, 8.8]
container[::3]
[0.0, 3.3, 6.6, 9.9]
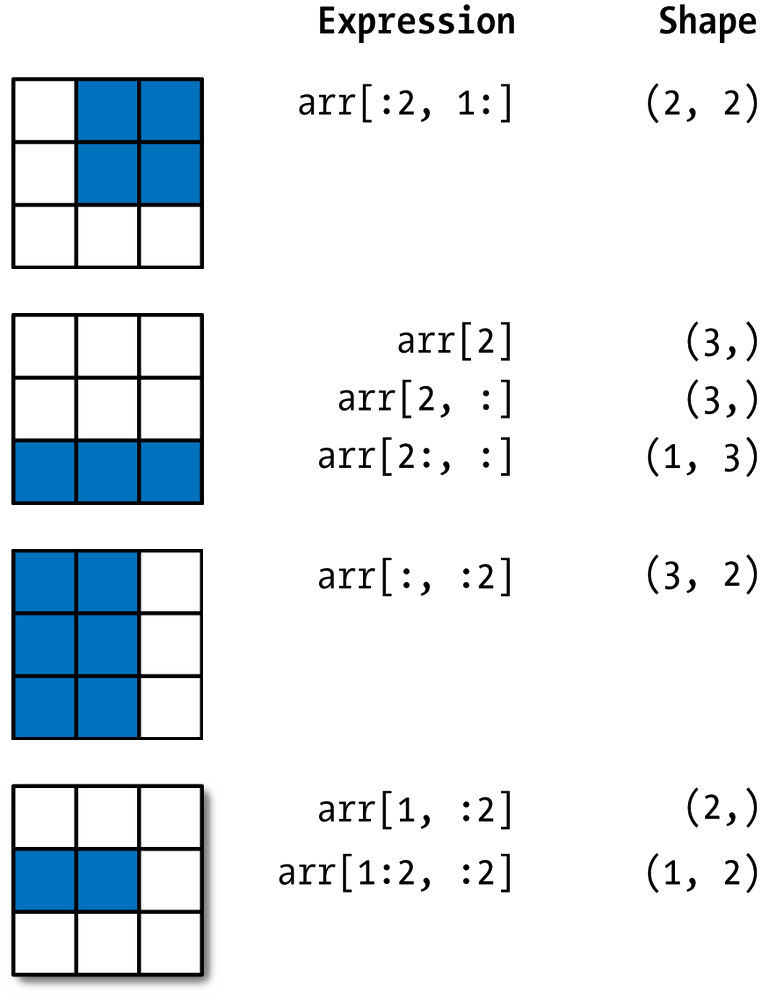
NumPy arrays can be sliced like this, but they can also include a comma (,) to slice over multiple dimensions.
arr = np.array([[1.1, 2.2, 3.3],
[4.4, 5.5, 6.6],
[7.7, 8.8, 9.9]])
arr
array([[1.1, 2.2, 3.3],
[4.4, 5.5, 6.6],
[7.7, 8.8, 9.9]])
arr[:2, 1:]
array([[2.2, 3.3],
[5.5, 6.6]])
arr[2:, :]
array([[7.7, 8.8, 9.9]])
arr[:, :2]
array([[1.1, 2.2],
[4.4, 5.5],
[7.7, 8.8]])
arr[1:2, :2]
array([[4.4, 5.5]])
Mini-quiz 1: Given this 3D array,
array3d = np.arange(2 * 3 * 5).reshape(2, 3, 5)
array3d
array([[[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]],
[[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29]]])
you can select items
with
array3d[:, 1:, 1:]
array([[[ 6, 7, 8, 9],
[11, 12, 13, 14]],
[[21, 22, 23, 24],
[26, 27, 28, 29]]])
Write a slice that selects these elements:
Mini-quiz 2: Use slicing and elementwise subtraction (-) together to find the sizes of the spaces between consecutive elements in the following array. (They’re all 1.1.)
array = np.array([1.1, 2.2, 3.3, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9])
array
array([1.1, 2.2, 3.3, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9])
Hint:
Advanced slicing#
In addition, NumPy can slice arrays with arrays. If the array in square brackets ([ ]) has boolean values, it must have the same length (shape) as the array to slice and items that line up with True are kept; items that line up with False are dropped.
arr = np.array([ 0.0, 1.1, 2.2, 3.3, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9])
mask = np.array([False, False, False, False, False, True, False, True, False, True])
# 5.5 7.7 9.9
arr[mask]
array([5.5, 7.7, 9.9])
In particle physics, this is usually used to select events, as a cut.
cut = arr > 3
cut
array([False, False, False, True, True, True, True, True, True,
True])
arr[cut]
array([3.3, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9])
If the array in square brackets ([ ]) has integer values, it picks out elements by index.
arr[np.array([5, 7, -1])]
array([5.5, 7.7, 9.9])
Unlike boolean-masking, the items to select can be out of order.
arr[np.array([-1, 7, 5])]
array([9.9, 7.7, 5.5])
And they can also include duplicates.
arr[np.array([-1, -1, -1, 7, 7, 5])]
array([9.9, 9.9, 9.9, 7.7, 7.7, 5.5])
Integer array slicing is the most general kind of slicing: if you think of an array as a function from index position (integers) to values, integer array slicing is function composition. Consider this example of text vectorization:
text = """
WOULD YOU LIKE GREEN EGGS AND HAM?
I DO NOT LIKE THEM, SAM-I-AM.
I DO NOT LIKE GREEN EGGS AND HAM.
WOULD YOU LIKE THEM HERE OR THERE?
I WOULD NOT LIKE THEM HERE OR THERE.
I WOULD NOT LIKE THEM ANYWHERE.
I DO NOT LIKE GREEN EGGS AND HAM.
I DO NOT LIKE THEM, SAM-I-AM.
WOULD YOU LIKE THEM IN A HOUSE?
WOULD YOU LIKE THEN WITH A MOUSE?
I DO NOT LIKE THEM IN A HOUSE.
I DO NOT LIKE THEM WITH A MOUSE.
I DO NOT LIKE THEM HERE OR THERE.
I DO NOT LIKE THEM ANYWHERE.
I DO NOT LIKE GREEN EGGS AND HAM.
I DO NOT LIKE THEM, SAM-I-AM.
WOULD YOU EAT THEM IN A BOX?
WOULD YOU EAT THEM WITH A FOX?
NOT IN A BOX. NOT WITH A FOX.
NOT IN A HOUSE. NOT WITH A MOUSE.
I WOULD NOT EAT THEM HERE OR THERE.
I WOULD NOT EAT THEM ANYWHERE.
I WOULD NOT EAT GREEN EGGS AND HAM.
I DO NOT LIKE THEM, SAM-I-AM.
"""
# remove punctuation and make an array of words
words = np.array(text.replace(",", " ").replace(".", " ").replace("?", " ").replace("!", " ").replace("-", " ").split())
# find the unique words and get an index of where they are in the corpus
dictionary, index = np.unique(words, return_inverse=True)
dictionary
array(['A', 'AM', 'AND', 'ANYWHERE', 'BOX', 'DO', 'EAT', 'EGGS', 'FOX',
'GREEN', 'HAM', 'HERE', 'HOUSE', 'I', 'IN', 'LIKE', 'MOUSE', 'NOT',
'OR', 'SAM', 'THEM', 'THEN', 'THERE', 'WITH', 'WOULD', 'YOU'],
dtype='<U8')
index
array([24, 25, 15, 9, 7, 2, 10, 13, 5, 17, 15, 20, 19, 13, 1, 13, 5,
17, 15, 9, 7, 2, 10, 24, 25, 15, 20, 11, 18, 22, 13, 24, 17, 15,
20, 11, 18, 22, 13, 24, 17, 15, 20, 3, 13, 5, 17, 15, 9, 7, 2,
10, 13, 5, 17, 15, 20, 19, 13, 1, 24, 25, 15, 20, 14, 0, 12, 24,
25, 15, 21, 23, 0, 16, 13, 5, 17, 15, 20, 14, 0, 12, 13, 5, 17,
15, 20, 23, 0, 16, 13, 5, 17, 15, 20, 11, 18, 22, 13, 5, 17, 15,
20, 3, 13, 5, 17, 15, 9, 7, 2, 10, 13, 5, 17, 15, 20, 19, 13,
1, 24, 25, 6, 20, 14, 0, 4, 24, 25, 6, 20, 23, 0, 8, 17, 14,
0, 4, 17, 23, 0, 8, 17, 14, 0, 12, 17, 23, 0, 16, 13, 24, 17,
6, 20, 11, 18, 22, 13, 24, 17, 6, 20, 3, 13, 24, 17, 6, 9, 7,
2, 10, 13, 5, 17, 15, 20, 19, 13, 1])
The index is a vector encoding the text corpus. The first few words are
dictionary[index[0]]
np.str_('WOULD')
dictionary[index[1]]
np.str_('YOU')
dictionary[index[2]]
np.str_('LIKE')
and the whole text is
dictionary[index]
array(['WOULD', 'YOU', 'LIKE', 'GREEN', 'EGGS', 'AND', 'HAM', 'I', 'DO',
'NOT', 'LIKE', 'THEM', 'SAM', 'I', 'AM', 'I', 'DO', 'NOT', 'LIKE',
'GREEN', 'EGGS', 'AND', 'HAM', 'WOULD', 'YOU', 'LIKE', 'THEM',
'HERE', 'OR', 'THERE', 'I', 'WOULD', 'NOT', 'LIKE', 'THEM', 'HERE',
'OR', 'THERE', 'I', 'WOULD', 'NOT', 'LIKE', 'THEM', 'ANYWHERE',
'I', 'DO', 'NOT', 'LIKE', 'GREEN', 'EGGS', 'AND', 'HAM', 'I', 'DO',
'NOT', 'LIKE', 'THEM', 'SAM', 'I', 'AM', 'WOULD', 'YOU', 'LIKE',
'THEM', 'IN', 'A', 'HOUSE', 'WOULD', 'YOU', 'LIKE', 'THEN', 'WITH',
'A', 'MOUSE', 'I', 'DO', 'NOT', 'LIKE', 'THEM', 'IN', 'A', 'HOUSE',
'I', 'DO', 'NOT', 'LIKE', 'THEM', 'WITH', 'A', 'MOUSE', 'I', 'DO',
'NOT', 'LIKE', 'THEM', 'HERE', 'OR', 'THERE', 'I', 'DO', 'NOT',
'LIKE', 'THEM', 'ANYWHERE', 'I', 'DO', 'NOT', 'LIKE', 'GREEN',
'EGGS', 'AND', 'HAM', 'I', 'DO', 'NOT', 'LIKE', 'THEM', 'SAM', 'I',
'AM', 'WOULD', 'YOU', 'EAT', 'THEM', 'IN', 'A', 'BOX', 'WOULD',
'YOU', 'EAT', 'THEM', 'WITH', 'A', 'FOX', 'NOT', 'IN', 'A', 'BOX',
'NOT', 'WITH', 'A', 'FOX', 'NOT', 'IN', 'A', 'HOUSE', 'NOT',
'WITH', 'A', 'MOUSE', 'I', 'WOULD', 'NOT', 'EAT', 'THEM', 'HERE',
'OR', 'THERE', 'I', 'WOULD', 'NOT', 'EAT', 'THEM', 'ANYWHERE', 'I',
'WOULD', 'NOT', 'EAT', 'GREEN', 'EGGS', 'AND', 'HAM', 'I', 'DO',
'NOT', 'LIKE', 'THEM', 'SAM', 'I', 'AM'], dtype='<U8')
Reductions#
Reductions are operations that reduce the number of dimensions in an array.
arr = np.array([[ 1, 2, 3, 4],
[ 10, 20, 30, 40],
[100, 200, 300, 400]])
In a sense, scalar-integer slicing is a reduction:
arr[2, :]
array([100, 200, 300, 400])
arr[:, 3]
array([ 4, 40, 400])
A scalar is a zero-dimensional array, so this is also reduction:
arr[2, 3]
np.int64(400)
But it’s more common to refer to operations like sum, min/max, and mean as reductions.
By default, they reduce to a scalar.
np.sum(arr)
np.int64(1110)
np.max(arr)
np.int64(400)
But they can also reduce along one of the dimensions.
np.sum(arr, axis=0)
array([111, 222, 333, 444])
np.sum(arr, axis=1)
array([ 10, 100, 1000])
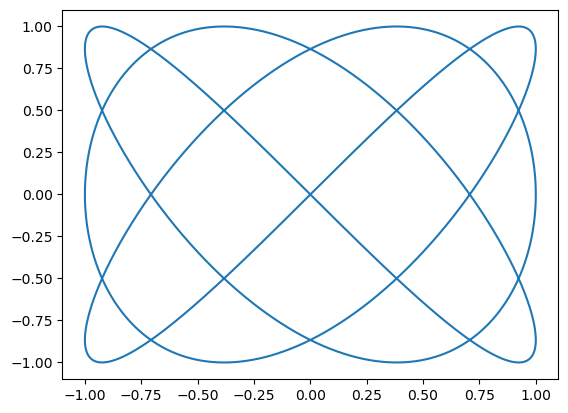
Mini-quiz 3: Using slicing, elementwise operations, and a reducer, find the length of this curve.
t = np.linspace(0, 2*np.pi, 10000)
x = np.sin(3*t)
y = np.sin(4*t)
plt.plot(x, y);
Lesson 2 project: Higgs decays from arrays#
As described in the intro, navigate to the notebooks directory and open lesson-2-project.ipynb, then follow its instructions.