Arreglos irregulares, desiguales y Awkward Array#
¿Qué es Awkward Array?#
La lección anterior incluía un corte complicado:
corte = muones["nMuon"] == 2
pt0 = muones["Muon_pt", corte, 0]
Las tres partes de muones["Muon_pt", corte, 0] son:
selecciona el campo
"Muon_pt"de todos los registros en la matriz,aplica
corte, una matriz booleana, para seleccionar solo los eventos con dos muones,selecciona el primer (
0) muón de cada uno de esos pares. De manera similar, para el segundo (1) muón.
NumPy no podría realizar un corte así, ni siquiera representar una matriz de listas de longitud variable sin recurrir a arreglos de objetos.
import numpy as np
np.array([[0.0, 1.1, 2.2], [], [3.3, 4.4], [5.5], [6.6, 7.7, 8.8, 9.9]])
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[1], line 3
1 import numpy as np
----> 3 np.array([[0.0, 1.1, 2.2], [], [3.3, 4.4], [5.5], [6.6, 7.7, 8.8, 9.9]])
ValueError: setting an array element with a sequence. The requested array has an inhomogeneous shape after 1 dimensions. The detected shape was (5,) + inhomogeneous part.
Awkward Array está diseñado para llenar este vacío:
import awkward as ak
ak.Array([[0.0, 1.1, 2.2], [], [3.3, 4.4], [5.5], [6.6, 7.7, 8.8, 9.9]])
[[0, 1.1, 2.2], [], [3.3, 4.4], [5.5], [6.6, 7.7, 8.8, 9.9]] ----------------------- type: 5 * var * float64
Arreglos como este se llaman “irregulares” o “desiguales” (en inglés, “jagged arrays” o a veces “ragged arrays”).
Rebanadas en Awkward Array#
Las rebanadas básicas son una generalización de los de NumPy. Lo que NumPy haría si tuviera listas de longitud variable.
array = ak.Array([[0.0, 1.1, 2.2], [], [3.3, 4.4], [5.5], [6.6, 7.7, 8.8, 9.9]])
array.tolist()
[[0.0, 1.1, 2.2], [], [3.3, 4.4], [5.5], [6.6, 7.7, 8.8, 9.9]]
array[2]
[3.3, 4.4] ----------------- type: 2 * float64
array[-1, 1]
np.float64(7.7)
array[2:, 0]
[3.3, 5.5, 6.6] ----------------- type: 3 * float64
array[2:, 1:]
[[4.4], [], [7.7, 8.8, 9.9]] ----------------------- type: 3 * var * float64
array[:, 0]
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
Cell In[8], line 1
----> 1 array[:, 0]
File ~/miniconda3/envs/skhep-tutorial/lib/python3.12/site-packages/awkward/highlevel.py:1066, in Array.__getitem__(self, where)
636 """
637 Args:
638 where (many types supported; see below): Index of positions to
(...) 1062 have the same dimension as the array being indexed.
1063 """
1064 with ak._errors.SlicingErrorContext(self, where):
1065 return wrap_layout(
-> 1066 prepare_layout(self._layout[where]),
1067 self._behavior,
1068 allow_other=True,
1069 attrs=self._attrs,
1070 )
File ~/miniconda3/envs/skhep-tutorial/lib/python3.12/site-packages/awkward/contents/content.py:512, in Content.__getitem__(self, where)
511 def __getitem__(self, where):
--> 512 return self._getitem(where)
File ~/miniconda3/envs/skhep-tutorial/lib/python3.12/site-packages/awkward/contents/content.py:557, in Content._getitem(self, where)
548 nextwhere = ak._slicing.prepare_advanced_indexing(items, backend)
550 next = ak.contents.RegularArray(
551 this,
552 this.length,
553 1,
554 parameters=None,
555 )
--> 557 out = next._getitem_next(nextwhere[0], nextwhere[1:], None)
559 if out.length is not unknown_length and out.length == 0:
560 return out._getitem_nothing()
File ~/miniconda3/envs/skhep-tutorial/lib/python3.12/site-packages/awkward/contents/regulararray.py:518, in RegularArray._getitem_next(self, head, tail, advanced)
512 nextcontent = self._content._carry(nextcarry, True)
514 if advanced is None or (
515 advanced.length is not unknown_length and advanced.length == 0
516 ):
517 return RegularArray(
--> 518 nextcontent._getitem_next(nexthead, nexttail, advanced),
519 nextsize,
520 self._length,
521 parameters=self._parameters,
522 )
523 else:
524 nextadvanced = ak.index.Index64.empty(nextcarry.length, index_nplike)
File ~/miniconda3/envs/skhep-tutorial/lib/python3.12/site-packages/awkward/contents/listarray.py:721, in ListArray._getitem_next(self, head, tail, advanced)
715 head = ak._slicing.normalize_integer_like(head)
716 assert (
717 nextcarry.nplike is self._backend.index_nplike
718 and self._starts.nplike is self._backend.index_nplike
719 and self._stops.nplike is self._backend.index_nplike
720 )
--> 721 self._maybe_index_error(
722 self._backend[
723 "awkward_ListArray_getitem_next_at",
724 nextcarry.dtype.type,
725 self._starts.dtype.type,
726 self._stops.dtype.type,
727 ](
728 nextcarry.data,
729 self._starts.data,
730 self._stops.data,
731 lenstarts,
732 head,
733 ),
734 slicer=head,
735 )
736 nextcontent = self._content._carry(nextcarry, True)
737 return nextcontent._getitem_next(nexthead, nexttail, advanced)
File ~/miniconda3/envs/skhep-tutorial/lib/python3.12/site-packages/awkward/contents/content.py:277, in Content._maybe_index_error(self, error, slicer)
275 else:
276 message = self._backend.format_kernel_error(error)
--> 277 raise ak._errors.index_error(self, slicer, message)
IndexError: cannot slice ListArray (of length 5) with array(0): index out of range while attempting to get index 0 (in compiled code: https://github.com/scikit-hep/awkward/blob/awkward-cpp-39/awkward-cpp/src/cpu-kernels/awkward_ListArray_getitem_next_at.cpp#L21)
This error occurred while attempting to slice
<Array [[0, 1.1, 2.2], ..., [6.6, 7.7, ..., 9.9]] type='5 * var * float64'>
with
(:, 0)
Quiz rápido: ¿por qué el último genera un error?
Las rebanadas con booleanos y enteros también funcionan.
array[[True, False, True, False, True]]
[[0, 1.1, 2.2], [3.3, 4.4], [6.6, 7.7, 8.8, 9.9]] ----------------------- type: 3 * var * float64
array[[2, 3, 3, 1]]
[[3.3, 4.4], [5.5], [5.5], []] ----------------------- type: 4 * var * float64
Como en NumPy, se pueden calcular arreglos booleanos para rebanadas, y funciones como ak.num son útiles para eso.
ak.num(array)
[3, 0, 2, 1, 4] --------------- type: 5 * int64
ak.num(array) > 0
[True, False, True, True, True] -------------- type: 5 * bool
array[ak.num(array) > 0, 0]
[0, 3.3, 5.5, 6.6] ----------------- type: 4 * float64
array[ak.num(array) > 1, 1]
[1.1, 4.4, 7.7] ----------------- type: 3 * float64
Ahora considera esto (similar a un ejemplo de la primera lección):
corte = array * 10 % 2 == 0
array[corte]
[[0, 2.2], [], [4.4], [], [6.6, 8.8]] ----------------------- type: 5 * var * float64
Este arreglo, corte, no es solo un arreglo de booleanos. Es un arreglo irrecular de booleanos. Todas sus listas anidadas encajan en las listas anidadas de array, por lo que puede seleccionar profundamente números, en lugar de seleccionar listas.
Aplicación: seleccionando partículas, en lugar de eventos#
Volviendo al TTree grande de la lección anterior,
import uproot
archivo = uproot.open(
"root://eospublic.cern.ch//eos/opendata/cms/derived-data/AOD2NanoAODOutreachTool/Run2012BC_DoubleMuParked_Muons.root"
)
tree = archivo["Events"]
muon_pt = tree["Muon_pt"].array(entry_stop=10)
muon_pt
[[10.8, 15.7], [10.5, 16.3], [3.28], [11.4, 17.6, 9.62, 3.5], [3.28, 3.64, 32.9, 23.7], [3.57, 4.57, 4.37], [57.6, 53], [11.3, 23.9], [10.2, 14.2], [11.5, 3.47]] -------------------------- type: 10 * var * float32
Este arreglo irregular de booleanos selecciona todos los muones con al menos 20 GeV:
corte_particula = muon_pt > 20
muon_pt[corte_particula]
[[], [], [], [], [32.9, 23.7], [], [57.6, 53], [23.9], [], []] ------------------------ type: 10 * var * float32
y este arreglo de booleanos no irregular (hecho con ak.any) selecciona todos los eventos que tienen un muón con al menos 20 GeV:
corte_evento = ak.any(muon_pt > 20, axis=1)
muon_pt[corte_evento]
[[3.28, 3.64, 32.9, 23.7], [57.6, 53], [11.3, 23.9]] -------------------------- type: 3 * var * float32
Quiz rápido: construye exactamente el mismo corte_evento utilizando ak.max.
Quiz rápido: aplica ambos cortes; es decir, selecciona muones con más de 20 GeV de los eventos que los tienen.
Sugerencia: querrás hacer un
muones_seleccionados = muon_pt[corte_particula]
intermediario y no puedes usar la variable corte_evento tal como está.
Sugerencia: el resultado final debería ser un arreglo irregular, al igual que muon_pt, pero con menos listas y menos elementos en esas listas.
Solución
muones_seleccionados = muon_pt[corte_particula]
resultado_final = muones_seleccionados[corte_evento]
resultado_final.tolist()
Combinatoria en Awkward Array#
Las listas de longitud variable presentan más problemas que solo el corte y el cálculo de fórmulas en arrays. A menudo, queremos combinar partículas en todos los pares posibles (dentro de cada evento) para buscar cadenas de descomposición.
Pares de dos arrays, pares de un solo array#
Awkward Array tiene funciones que generan estas combinaciones. Por ejemplo, ak.cartesian toma un producto cartesiano por evento (cuando axis=1, el valor predeterminado).
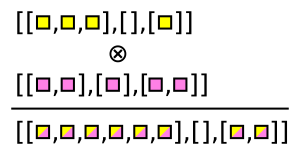
numeros = ak.Array([[1, 2, 3], [], [5, 7], [11]])
letras = ak.Array([["a", "b"], ["c"], ["d"], ["e", "f"]])
pares = ak.cartesian((numeros, letras))
pares
[[(1, 'a'), (1, 'b'), (2, 'a'), (2, 'b'), (3, 'a'), (3, 'b')],
[],
[(5, 'd'), (7, 'd')],
[(11, 'e'), (11, 'f')]]
--------------------------------------------------------------
type: 4 * var * (
int64,
string
)Estos pares son 2-tuplas, que son como registros en cómo se extraen de un array: usando cadenas.
pares["0"]
[[1, 1, 2, 2, 3, 3], [], [5, 7], [11, 11]] --------------------- type: 4 * var * int64
pares["1"]
[['a', 'b', 'a', 'b', 'a', 'b'], [], ['d', 'd'], ['e', 'f']] -------------------------------- type: 4 * var * string
También hay ak.unzip, que extrae cada campo en un array separado (lo opuesto de ak.zip).
izquierda, derecha = ak.unzip(pares)
izquierda
[[1, 1, 2, 2, 3, 3], [], [5, 7], [11, 11]] --------------------- type: 4 * var * int64
derecha
[['a', 'b', 'a', 'b', 'a', 'b'], [], ['d', 'd'], ['e', 'f']] -------------------------------- type: 4 * var * string
Tenga en cuenta que estos izquierda y derecha no son los numeros y letras originales: han sido duplicados y tienen la misma forma.
El producto cartesiano es equivalente a este bucle for en C++ sobre dos colecciones:
for (int i = 0; i < numeros.size(); i++) {
for (int j = 0; j < letras.size(); j++) {
// formula con numeros[i] y letras[j]
}
}
A veces, sin embargo, queremos encontrar todos los pares dentro de una sola colección, sin repetición. Eso sería equivalente a este bucle for en C++:
for (int i = 0; i < numeros.size(); i++) {
for (int j = i + 1; i < numeros.size(); j++) {
// formula con numeros[i] y numeros[j]
}
}
La función Awkward para este caso es ak.combinations.

pares = ak.combinations(numeros, 2)
pares
[[(1, 2), (1, 3), (2, 3)],
[],
[(5, 7)],
[]]
--------------------------
type: 4 * var * (
int64,
int64
)izquierda, derecha = ak.unzip(pares)
izquierda * derecha # Se alinean, por lo que podemos calcular fórmulas
[[2, 3, 6], [], [35], []] --------------------- type: 4 * var * int64
Aplicación a los dimuones#
La búsqueda de dimuones en la lección anterior fue un poco ingenua en el sentido de que requeríamos exactamente dos muones en cada evento y solo calculamos la masa de esa combinación. Si hubiera un tercer muón presente debido a una compleja descomposición electrodébil o porque algo fue medido incorrectamente, estaríamos ciegos a los otros dos muones. Podrían ser dimuones reales.
Un mejor procedimiento sería buscar todos los pares de muones en un evento y aplicar algunos criterios para seleccionarlos.
En este ejemplo, juntaremos (usando ak.zip) las variables de los muones en registros.
import uproot
import awkward as ak
archivo = uproot.open(
"root://eospublic.cern.ch//eos/opendata/cms/derived-data/AOD2NanoAODOutreachTool/Run2012BC_DoubleMuParked_Muons.root"
)
tree = archivo["Events"]
arrays = tree.arrays(filter_name="/Muon_(pt|eta|phi|charge)/", entry_stop=10000)
muones = ak.zip(
{
"pt": arrays["Muon_pt"],
"eta": arrays["Muon_eta"],
"phi": arrays["Muon_phi"],
"charge": arrays["Muon_charge"],
}
)
print(arrays.type)
print(muones.type)
10000 * {Muon_pt: var * float32, Muon_eta: var * float32, Muon_phi: var * float32, Muon_charge: var * int32}
10000 * var * {pt: float32, eta: float32, phi: float32, charge: int32}
La diferencia entre arrays y muones es que arrays contiene listas separadas de "Muon_pt", "Muon_eta", "Muon_phi", "Muon_charge", mientras que muones contiene listas de registros con los campos "pt", "eta", "phi", "charge".
Ahora podemos calcular pares de objetos muones.
pares = ak.combinations(muones, 2)
pares.type
ArrayType(ListType(RecordType([RecordType([NumpyType('float32'), NumpyType('float32'), NumpyType('float32'), NumpyType('int32')], ['pt', 'eta', 'phi', 'charge']), RecordType([NumpyType('float32'), NumpyType('float32'), NumpyType('float32'), NumpyType('int32')], ['pt', 'eta', 'phi', 'charge'])], None)), 10000, None)
y separarlos en arreglos del primer muón y del segundo muón en cada par.
mu1, mu2 = ak.unzip(pares)
Quiz rápido: ¿cómo garantizarías que todas las listas de registros en mu1 y mu2 tengan las mismas longitudes? Sugerencia: consulta ak.num y ak.all.
Dado que tienen las mismas longitudes, podemos usarlos en una fórmula.
import numpy as np
masa = np.sqrt(
2 * mu1.pt * mu2.pt * (np.cosh(mu1.eta - mu2.eta) - np.cos(mu1.phi - mu2.phi))
)
Quiz rápido: ¿cuántas masas tenemos en cada evento? ¿Cómo se compara esto con muons, mu1 y mu2?
Graficando el arreglo irregular#
Dado que esta masa es un arreglo irregular, no se puede histogramar directamente. Los histogramas toman un conjunto de números como entradas, pero este arreglo contiene listas.
Suponiendo que solo deseas graficar los números de las listas, puedes usar ak.flatten para aplanar un nivel de lista o ak.ravel para aplanar todos los niveles.
import hist
hist.Hist(hist.axis.Regular(120, 0, 120, label="masa [GeV]")).fill(
ak.ravel(masa)
).plot()
[StairsArtists(stairs=<matplotlib.patches.StepPatch object at 0x7f127493b710>, errorbar=<ErrorbarContainer object of 3 artists>, legend_artist=<ErrorbarContainer object of 3 artists>)]
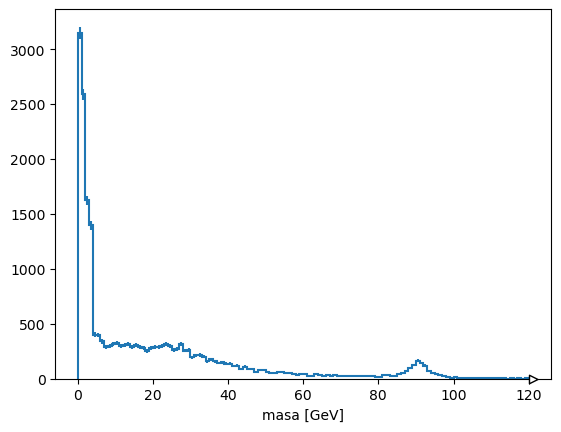
Alternativamente, supongamos que deseas graficar la máxima masa candidata en cada evento, sesgándola hacia los bosones Z. ak.max es una función diferente que selecciona un elemento de cada lista, cuando se utiliza con axis=1.
ak.max(masa, axis=1)
[34.4, 27.9, None, 26.2, 18.2, 4.52, 114, 1.57, 23.7, 0.696, ..., 3.36, 3.53, 4.26, 3.05, 2.2, 24.2, 42.9, 0.252, 93.4] ---------------------- type: 10000 * ?float32
Algunos valores son None porque no hay un máximo en una lista vacía. ak.flatten/ak.ravel eliminan los valores faltantes (None) así como aplastan las listas,
ak.flatten(ak.max(masa, axis=1), axis=0)
[34.4, 27.9, 26.2, 18.2, 4.52, 114, 1.57, 23.7, 0.696, 27.1, ..., 3.36, 3.53, 4.26, 3.05, 2.2, 24.2, 42.9, 0.252, 93.4] -------------------- type: 8880 * float32
pero también lo hace eliminar las listas vacías en primer lugar.
ak.max(masa[ak.num(masa) > 0], axis=1)
[34.4, 27.9, 26.2, 18.2, 4.52, 114, 1.57, 23.7, 0.696, 27.1, ..., 3.36, 3.53, 4.26, 3.05, 2.2, 24.2, 42.9, 0.252, 93.4] --------------------- type: 8880 * ?float32
Ejercicio: seleccionar pares de muones con cargas opuestas
Este no es un corte a nivel de evento ni un corte a nivel de partículas, es un corte sobre pares de partículas.
Las variables mu1 y mu2 son las mitades izquierda y derecha de los pares de muones. Por lo tanto,
corte = (mu1.charge != mu2.charge)
tiene la multiplicidad correcta para aplicarse a la matriz masa.
hist.Hist(hist.axis.Regular(120, 0, 120, label="masa [GeV]")).fill(
ak.ravel(mass[cut])
).plot()
plotea los pares de muones seleccionados.
Ejercicio (más difícil): traza el candidato a masa por evento que esté estrictamente más cercano a la masa del Z
En lugar de solo tomar la masa máxima en cada evento, encuentra la que tenga la diferencia mínima entre la masa calculada y masa_z = 91.
Sugerencia: usa ak.argmin con keepdims=True.
Anticipando una de las futuras lecciones, podrías obtener una masa más precisa pidiendo a la librería Particle:
import particle, hepunits
masa_z = particle.Particle.findall("Z0")[0].mass / hepunits.GeV
En lugar de maximizar masa, queremos minimizar abs(masa - masa_z) y aplicar esa elección a masa. ak.argmin devuelve la posición del índice de esta diferencia mínima, que luego podemos aplicar a la masa original. Sin embargo, sin keepdims=True, ak.argmin elimina la dimensión que necesitaríamos para que esta matriz tenga la misma forma anidada que masa. Por lo tanto, usamos keepdims=True y luego utilizamos ak.ravel para deshacernos de los valores faltantes y aplanar las listas.
El último paso requeriría dos aplicaciones de ak.flatten: una para aplastar listas en el primer nivel y otra para eliminar None en el segundo nivel.
cual = ak.argmin(abs(masa - masa_z), axis=1, keepdims=True)
hist.Hist(hist.axis.Regular(120, 0, 120, label="masa [GeV]")).fill(
ak.ravel(masa[cual])
).plot()
