Detalles de TTree#
Estructura y terminología de archivos ROOT#
Un archivo ROOT (ROOT TFile, uproot.ReadOnlyFile) es como un pequeño sistema de archivos que contiene directorios anidados (ROOT TDirectory, uproot.ReadOnlyDirectory). En Uproot, los directorios anidados se presentan como diccionarios anidados.
Cualquier instancia de clase (ROOT TObject, uproot.Model) puede almacenarse en un directorio, incluidos tipos como histogramas (por ejemplo, ROOT TH1, uproot.behaviors.TH1.TH1).
Una de estas clases, TTree (ROOT TTree, uproot.TTree), es una puerta de entrada a conjuntos de datos grandes. Un TTree es algo parecido a un DataFrame de Pandas en el sentido de que representa una tabla de datos. Las columnas se llaman TBranches (ROOT TBranch, uproot.TBranch), que pueden ser anidadas (a diferencia de Pandas), y los datos pueden tener cualquier tipo de C++ (a diferencia de Pandas, que puede almacenar cualquier tipo de Python).
Un TTree a menudo es demasiado grande para caber en la memoria, y a veces (raramente) incluso una sola TBranch es demasiado grande para caber en la memoria. Cada TBranch se divide en TBaskets (ROOT TBasket, uproot.models.TBasket.Model_TBasket), que son “lotes” de datos. (Estos son los mismos lotes que cada llamada a extend escribe en la lección anterior.) Los TBaskets son la unidad más pequeña que se puede leer de un TTree: si deseas leer la primera entrada, debes leer el primer TBasket.
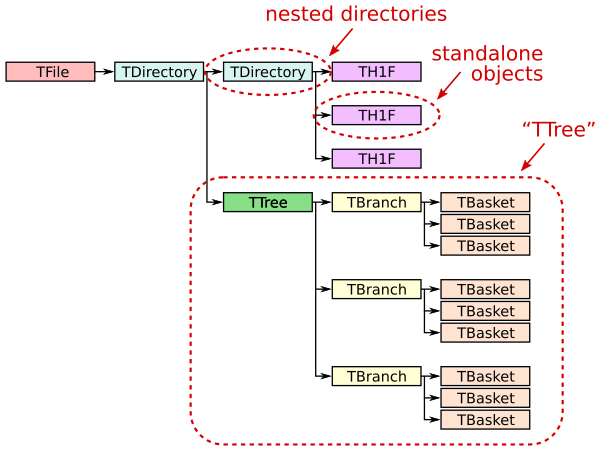
Como analista de datos, probablemente te ocuparás de los TTrees y TBranches de manera directa, pero solo de los TBaskets cuando surjan problemas de eficiencia. Los archivos con TBaskets grandes pueden requerir mucha memoria para leer; los archivos con TBaskets pequeños serán más lentos de leer (en ROOT también, pero especialmente en Uproot). Los TBaskets del tamaño de megabytes suelen ser ideales.
Ejemplos con un TTree grande#
Este archivo tiene 2.1 GB y está alojado en el Portal de Datos Abiertos de CERN.
import uproot
archivo = uproot.open(
"root://eospublic.cern.ch//eos/opendata/cms/derived-data/AOD2NanoAODOutreachTool/Run2012BC_DoubleMuParked_Muons.root"
)
archivo.classnames()
{'Events;75': 'TTree', 'Events;74': 'TTree'}
¿Por qué el ;74 y ;75?
Tal vez te hayas preguntado sobre los números después de los puntos y comas. Estos son los “números de ciclo” de ROOT, que permiten distinguir objetos con el mismo nombre. Se utilizan cuando un objeto necesita sobrescribirse a medida que crece sin perder la última copia válida de ese objeto, de modo que un archivo ROOT pueda leerse incluso si el proceso de escritura falló a mitad de camino.
En este caso, la última versión de este TTree es el número 75, y el número 74 es la penúltima.
Si no especificas números de ciclo, Uproot seleccionará el último por ti, lo cual es casi siempre lo que deseas. (En otras palabras, puedes ignorarlos.)
Simplemente solicitando el objeto uproot.TTree e imprimiendolo no lee todo el conjunto de datos.
tree = archivo["Events"]
tree.show()
name | typename | interpretation
---------------------+--------------------------+-------------------------------
nMuon | uint32_t | AsDtype('>u4')
Muon_pt | float[] | AsJagged(AsDtype('>f4'))
Muon_eta | float[] | AsJagged(AsDtype('>f4'))
Muon_phi | float[] | AsJagged(AsDtype('>f4'))
Muon_mass | float[] | AsJagged(AsDtype('>f4'))
Muon_charge | int32_t[] | AsJagged(AsDtype('>i4'))
Leyendo una parte de un TTree#
En la lección anterior, aprendimos que la forma más directa de leer una TBranch es llamando a uproot.TBranch.array.
tree["nMuon"].array()
[2, 2, 1, 4, 4, 3, 2, 2, 2, 2, ..., 2, 2, 2, 3, 2, 2, 4, 3, 2] ----------------------- type: 61540413 * uint32
Sin embargo, toma mucho tiempo porque se tiene que enviar una gran cantidad de datos a través de la red.
Para limitar la cantidad de datos leídos, establece entry_start y entry_stop en el rango que desees. El entry_start es inclusivo, entry_stop es exclusivo, y la primera entrada se indexaría por 0, al igual que los cortes en una interfaz de arreglo (primera lección). Uproot solo lee la cantidad de TBaskets necesarias para proporcionar estas entradas.
tree["nMuon"].array(entry_start=1_000, entry_stop=2_000)
[2, 2, 2, 2, 2, 2, 2, 2, 1, 2, ..., 2, 2, 2, 4, 4, 1, 3, 4, 3] ------------------- type: 1000 * uint32
Estos son los bloques de construcción de un lector de datos en paralelo: cada uno es responsable de un fragmento diferente. (Consulta también uproot.TTree.num_entries_for y uproot.TTree.common_entry_offsets, que se pueden usar para elegir entry_start/entry_stop de manera óptima.)
Leer múltiples TBranches a la vez#
Supongamos que sabes que necesitarás todos los TBranches de muones. Pedirlos en una sola solicitud es más eficiente que solicitarlos individualmente, porque el servidor puede estar trabajando en la lectura de los TBaskets posteriores del disco mientras los TBaskets anteriores se envían a ti a través de la red. Mientras que un TBranch tiene un método array, el TTree tiene un método arrays (en plural) para obtener múltiples arreglos.
muones = tree.arrays(
["Muon_pt", "Muon_eta", "Muon_phi", "Muon_mass", "Muon_charge"], entry_stop=1_000
)
muones
[{Muon_pt: [10.8, 15.7], Muon_eta: [1.07, -0.564], Muon_phi: [...], ...},
{Muon_pt: [10.5, 16.3], Muon_eta: [-0.428, ...], Muon_phi: [...], ...},
{Muon_pt: [3.28], Muon_eta: [2.21], Muon_phi: [-1.22], Muon_mass: ..., ...},
{Muon_pt: [11.4, 17.6, 9.62, 3.5], Muon_eta: [-1.59, ...], Muon_phi: ..., ...},
{Muon_pt: [3.28, 3.64, 32.9, 23.7], Muon_eta: [-2.17, ...], ...},
{Muon_pt: [3.57, 4.57, 4.37], Muon_eta: [-1.37, ...], Muon_phi: [...], ...},
{Muon_pt: [57.6, 53], Muon_eta: [-0.532, -1], Muon_phi: [...], ...},
{Muon_pt: [11.3, 23.9], Muon_eta: [-0.772, ...], Muon_phi: [...], ...},
{Muon_pt: [10.2, 14.2], Muon_eta: [0.442, 0.702], Muon_phi: [...], ...},
{Muon_pt: [11.5, 3.47], Muon_eta: [2.34, 2.35], Muon_phi: [...], ...},
...,
{Muon_pt: [3.13, 16.9, 11], Muon_eta: [-1.43, ...], Muon_phi: [...], ...},
{Muon_pt: [34.2, 14], Muon_eta: [-0.913, ...], Muon_phi: [...], ...},
{Muon_pt: [14, 8.19], Muon_eta: [-0.409, ...], Muon_phi: [...], ...},
{Muon_pt: [30.6], Muon_eta: [0.696], Muon_phi: [-1.95], Muon_mass: ..., ...},
{Muon_pt: [22.1, 12.9, 13.4], Muon_eta: [1.97, ...], Muon_phi: [...], ...},
{Muon_pt: [10.1, 4.34], Muon_eta: [0.833, 1.95], Muon_phi: [...], ...},
{Muon_pt: [4.36, 15.1, 12.4], Muon_eta: [1.05, ...], Muon_phi: [...], ...},
{Muon_pt: [17.7, 4.61, 8.79, 5.14], Muon_eta: [0.587, ...], ...},
{Muon_pt: [28.9, 8.62, 4.51], Muon_eta: [0.917, ...], Muon_phi: [...], ...}]
--------------------------------------------------------------------------------
type: 1000 * {
Muon_pt: var * float32,
Muon_eta: var * float32,
Muon_phi: var * float32,
Muon_mass: var * float32,
Muon_charge: var * int32
}Ahora, los cinco TBranches están en la salida, muones, que es un Awkward Array. Un Awkward Array de múltiples TBranches tiene una interfaz similar a un diccionario, por lo que podemos obtener cada variable de él por
muones["Muon_pt"]
muones["Muon_eta"]
muones["Muon_phi"] # etc.
[[-0.0343, 2.54], [-0.275, 2.54], [-1.22], [-2.08, 0.251, -2.01, -1.85], [-2.37, -2.31, -0.975, -0.773], [-2.91, 2.46, -3.06], [-0.0718, 3.09], [-2.25, -2.18], [0.678, -2.03], [3.13, 3.02], ..., [-1.85, -1.34, -1.31], [-0.607, -0.493], [-0.855, 0.0452], [-1.95], [0.327, -2.64, -2.63], [-1.54, -0.078], [2.11, -2.16, 2.13], [-0.133, -2.39, -0.225, -1.42], [2.08, -1.63, -1.47]] -------------------------------- type: 1000 * var * float32
¡Cuidado! ¡Es tree.arrays lo que realmente lee los datos!
Si no tienes cuidado con la llamada a uproot.TTree.arrays, podrías terminar esperando mucho tiempo por datos que no necesitas o podrías quedarte sin memoria. Leer todo con
todo = tree.arrays()
y luego seleccionar los arrays que deseas generalmente no es una buena idea. Al menos, establece un entry_stop.
Selección de TBranches por nombre#
Supongamos que tienes muchos TBranches de muones y no quieres enumerarlos todos. Tanto uproot.TTree.keys como uproot.TTree.arrays aceptan un argumento filter_name que puede seleccionarlos de varias maneras (consulta la documentación). En particular, es recomendable usar primero keys para saber qué ramas coinciden con tu filtro, seguido de arrays para leerlas realmente.
tree.keys(filter_name="Muon_*")
['Muon_pt', 'Muon_eta', 'Muon_phi', 'Muon_mass', 'Muon_charge']
tree.arrays(filter_name="Muon_*", entry_stop=1_000)
[{Muon_pt: [10.8, 15.7], Muon_eta: [1.07, -0.564], Muon_phi: [...], ...},
{Muon_pt: [10.5, 16.3], Muon_eta: [-0.428, ...], Muon_phi: [...], ...},
{Muon_pt: [3.28], Muon_eta: [2.21], Muon_phi: [-1.22], Muon_mass: ..., ...},
{Muon_pt: [11.4, 17.6, 9.62, 3.5], Muon_eta: [-1.59, ...], Muon_phi: ..., ...},
{Muon_pt: [3.28, 3.64, 32.9, 23.7], Muon_eta: [-2.17, ...], ...},
{Muon_pt: [3.57, 4.57, 4.37], Muon_eta: [-1.37, ...], Muon_phi: [...], ...},
{Muon_pt: [57.6, 53], Muon_eta: [-0.532, -1], Muon_phi: [...], ...},
{Muon_pt: [11.3, 23.9], Muon_eta: [-0.772, ...], Muon_phi: [...], ...},
{Muon_pt: [10.2, 14.2], Muon_eta: [0.442, 0.702], Muon_phi: [...], ...},
{Muon_pt: [11.5, 3.47], Muon_eta: [2.34, 2.35], Muon_phi: [...], ...},
...,
{Muon_pt: [3.13, 16.9, 11], Muon_eta: [-1.43, ...], Muon_phi: [...], ...},
{Muon_pt: [34.2, 14], Muon_eta: [-0.913, ...], Muon_phi: [...], ...},
{Muon_pt: [14, 8.19], Muon_eta: [-0.409, ...], Muon_phi: [...], ...},
{Muon_pt: [30.6], Muon_eta: [0.696], Muon_phi: [-1.95], Muon_mass: ..., ...},
{Muon_pt: [22.1, 12.9, 13.4], Muon_eta: [1.97, ...], Muon_phi: [...], ...},
{Muon_pt: [10.1, 4.34], Muon_eta: [0.833, 1.95], Muon_phi: [...], ...},
{Muon_pt: [4.36, 15.1, 12.4], Muon_eta: [1.05, ...], Muon_phi: [...], ...},
{Muon_pt: [17.7, 4.61, 8.79, 5.14], Muon_eta: [0.587, ...], ...},
{Muon_pt: [28.9, 8.62, 4.51], Muon_eta: [0.917, ...], Muon_phi: [...], ...}]
--------------------------------------------------------------------------------
type: 1000 * {
Muon_pt: var * float32,
Muon_eta: var * float32,
Muon_phi: var * float32,
Muon_mass: var * float32,
Muon_charge: var * int32
}(También hay filter_typename y filter_branch para más opciones.)
Escalando, haciendo un gráfico#
La mejor manera de entender lo que estás haciendo es experimentar con conjuntos de datos pequeños y luego escalarlos. Aquí, tomamos 1000 eventos y calculamos las masas de dimuones.
muones = tree.arrays(entry_stop=1_000)
corte = muones["nMuon"] == 2
pt0 = muones["Muon_pt", corte, 0]
pt1 = muones["Muon_pt", corte, 1]
eta0 = muones["Muon_eta", corte, 0]
eta1 = muones["Muon_eta", corte, 1]
phi0 = muones["Muon_phi", corte, 0]
phi1 = muones["Muon_phi", corte, 1]
import numpy as np
masa = np.sqrt(2 * pt0 * pt1 * (np.cosh(eta0 - eta1) - np.cos(phi0 - phi1)))
import hist
histmasa = hist.Hist(hist.axis.Regular(120, 0, 120, label="masa [GeV]"))
histmasa.fill(masa)
histmasa.plot()
[StairsArtists(stairs=<matplotlib.patches.StepPatch object at 0x7fd1b172dfa0>, errorbar=<ErrorbarContainer object of 3 artists>, legend_artist=<ErrorbarContainer object of 3 artists>)]
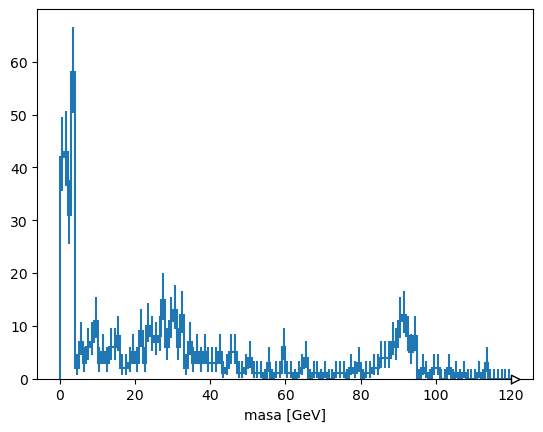
Eso funcionó (hay un pico en Z). Ahora, para hacer esto en todo el archivo, debemos tener más cuidado con lo que estamos leyendo.
tree.keys(filter_name=["nMuon", "/Muon_(pt|eta|phi)/"])
['nMuon', 'Muon_pt', 'Muon_eta', 'Muon_phi']
y acumular datos gradualmente con uproot.TTree.iterate. Esto maneja entry_start/entry_stop en un bucle.
histmasa = hist.Hist(hist.axis.Regular(120, 0, 120, label="masa [GeV]"))
for muones in tree.iterate(filter_name=["nMuon", "/Muon_(pt|eta|phi)/"]):
cut = muones["nMuon"] == 2
pt0 = muones["Muon_pt", cut, 0]
pt1 = muones["Muon_pt", cut, 1]
eta0 = muones["Muon_eta", cut, 0]
eta1 = muones["Muon_eta", cut, 1]
phi0 = muones["Muon_phi", cut, 0]
phi1 = muones["Muon_phi", cut, 1]
masa = np.sqrt(2 * pt0 * pt1 * (np.cosh(eta0 - eta1) - np.cos(phi0 - phi1)))
histmasa.fill(masa)
print(histmasa.sum() / tree.num_entries)
histmasa.plot()
0.02476806582367265
0.04953244301431646
0.07414066265691133
0.09883069845501362
0.12372555900786691
0.14857022490245556
0.1733401756663544
0.19790541542189521
0.2231366240587303
0.24903843268000167
0.2746961577914662
0.3004716591680982
0.3266033492495411
0.35272515964428125
0.37907369909915944
0.4053174618766371
0.4309308746433015
0.4559705993523313
0.4818679393653078
0.5026042967894935
[StairsArtists(stairs=<matplotlib.patches.StepPatch object at 0x7fd175a0eab0>, errorbar=<ErrorbarContainer object of 3 artists>, legend_artist=<ErrorbarContainer object of 3 artists>)]
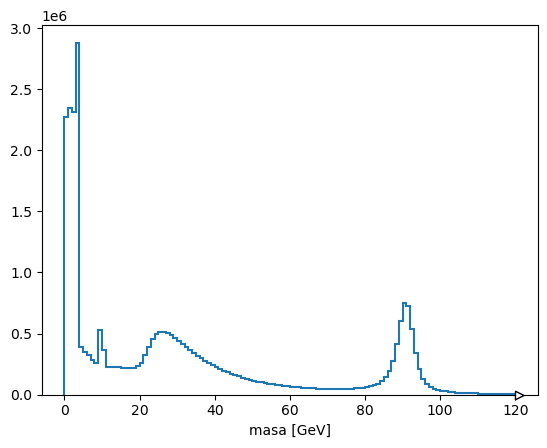
Obtener datos en NumPy o Pandas#
En todos los ejemplos anteriores, los métodos array, arrays e iterate devuelven arreglos Awkward. La biblioteca Awkward es útil para este tipo de datos (arreglos irregulares: más en la próxima lección), pero es posible que estés trabajando con bibliotecas que solo reconocen arreglos de NumPy o DataFrames de Pandas.
Utiliza library="np" o library="pd" para obtener NumPy o Pandas, respectivamente.
tree["nMuon"].array(library="np", entry_stop=10_000)
array([2, 2, 1, ..., 2, 2, 2], shape=(10000,), dtype=uint32)
tree.arrays(library="np", entry_stop=10_000)
{'nMuon': array([2, 2, 1, ..., 2, 2, 2], shape=(10000,), dtype=uint32),
'Muon_pt': array([array([10.763697, 15.736523], dtype=float32),
array([10.53849 , 16.327097], dtype=float32),
array([3.2753265], dtype=float32), ...,
array([30.238283, 13.035936], dtype=float32),
array([17.35597 , 15.874119], dtype=float32),
array([39.6421 , 42.273067], dtype=float32)],
shape=(10000,), dtype=object),
'Muon_eta': array([array([ 1.0668273, -0.5637865], dtype=float32),
array([-0.42778006, 0.34922507], dtype=float32),
array([2.2108555], dtype=float32), ...,
array([-1.1984524, -2.0278058], dtype=float32),
array([-0.83613676, -0.8279834 ], dtype=float32),
array([-2.090575 , -1.0396558], dtype=float32)],
shape=(10000,), dtype=object),
'Muon_phi': array([array([-0.03427272, 2.5426154 ], dtype=float32),
array([-0.2747921, 2.5397813], dtype=float32),
array([-1.2234136], dtype=float32), ...,
array([-2.2813563 , 0.60287297], dtype=float32),
array([-1.4231573, -1.4103615], dtype=float32),
array([ 2.2101276, -0.9990832], dtype=float32)],
shape=(10000,), dtype=object),
'Muon_mass': array([array([0.10565837, 0.10565837], dtype=float32),
array([0.10565837, 0.10565837], dtype=float32),
array([0.10565837], dtype=float32), ...,
array([0.10565837, 0.10565837], dtype=float32),
array([0.10565837, 0.10565837], dtype=float32),
array([0.10565837, 0.10565837], dtype=float32)],
shape=(10000,), dtype=object),
'Muon_charge': array([array([-1, -1], dtype=int32), array([ 1, -1], dtype=int32),
array([1], dtype=int32), ..., array([ 1, -1], dtype=int32),
array([ 1, -1], dtype=int32), array([ 1, -1], dtype=int32)],
shape=(10000,), dtype=object)}
tree.arrays(library="pd", entry_stop=10_000)
| nMuon | Muon_pt | Muon_eta | Muon_phi | Muon_mass | Muon_charge | |
|---|---|---|---|---|---|---|
| 0 | 2 | [10.763696670532227, 15.736522674560547] | [1.0668272972106934, -0.563786506652832] | [-0.03427272289991379, 2.5426154136657715] | [0.10565836727619171, 0.10565836727619171] | [-1, -1] |
| 1 | 2 | [10.538490295410156, 16.327096939086914] | [-0.42778006196022034, 0.34922507405281067] | [-0.2747921049594879, 2.539781332015991] | [0.10565836727619171, 0.10565836727619171] | [1, -1] |
| 2 | 1 | [3.2753264904022217] | [2.210855484008789] | [-1.2234135866165161] | [0.10565836727619171] | [1] |
| 3 | 4 | [11.429154396057129, 17.634033203125, 9.624728... | [-1.5882395505905151, -1.7511844635009766, -1.... | [-2.0773041248321533, 0.25135836005210876, -2.... | [0.10565836727619171, 0.10565836727619171, 0.1... | [1, 1, 1, 1] |
| 4 | 4 | [3.2834417819976807, 3.64400577545166, 32.9112... | [-2.1724836826324463, -2.18253493309021, -1.12... | [-2.3700082302093506, -2.3051390647888184, -0.... | [0.10565836727619171, 0.10565836727619171, 0.1... | [-1, -1, 1, 1] |
| ... | ... | ... | ... | ... | ... | ... |
| 9995 | 2 | [26.859142303466797, 9.353170394897461] | [1.930126667022705, 1.9606289863586426] | [2.006714105606079, 1.871167540550232] | [0.10565836727619171, 0.10565836727619171] | [1, -1] |
| 9996 | 2 | [9.003849029541016, 14.049983978271484] | [1.7759391069412231, 1.0048433542251587] | [-0.8459293246269226, 2.2061259746551514] | [0.10565836727619171, 0.10565836727619171] | [-1, 1] |
| 9997 | 2 | [30.238283157348633, 13.03593635559082] | [-1.198452353477478, -2.027805805206299] | [-2.2813563346862793, 0.6028729677200317] | [0.10565836727619171, 0.10565836727619171] | [1, -1] |
| 9998 | 2 | [17.35597038269043, 15.87411880493164] | [-0.8361367583274841, -0.8279833793640137] | [-1.4231573343276978, -1.4103615283966064] | [0.10565836727619171, 0.10565836727619171] | [1, -1] |
| 9999 | 2 | [39.6421012878418, 42.273067474365234] | [-2.0905749797821045, -1.0396558046340942] | [2.210127592086792, -0.9990832209587097] | [0.10565836727619171, 0.10565836727619171] | [1, -1] |
10000 rows × 6 columns
NumPy es excelente para datos no irregulares como la rama "nMuon", pero tiene que representar un número desconocido de muones por evento como un arreglo de arreglos de NumPy (es decir, objetos de Python).
Pandas se puede hacer representar múltiples partículas por evento colocando esta estructura en un pd.MultiIndex, pero no cuando el DataFrame contiene más de un tipo de partícula (por ejemplo, muones y electrones). Usa DataFrames separados para estos casos. Si ayuda, ten en cuenta que hay otra ruta a DataFrames: leyendo los datos como un Arreglo Awkward y llamando a ak.to_pandas sobre él. (Algunos métodos usan más memoria que otros, y he encontrado que Pandas es inusualmente intensivo en memoria.)
O usa Arreglos Awkward (próxima lección).
